佩特森-斯豪特定理

佩特森-斯豪特定理(Petersen-Schoute theorem)是關於三角形真正相似的傳遞定理，該定理斷言：若△ABC和△A′B′C′是真正相似三角形，並且△AA′A″，△BB′B″和△CC′C″也是真正相似三角形，則△A″B″C″和△ABC也是真正相似三角形。

基本介紹

• 中文名：佩特森-斯豪特定理
• 外文名：Petersen-Schoute theorem
• 所屬學科：數學
• 所屬問題：平面幾何（三角形）
• 簡介：關於三角形真正相似的傳遞定理
• 提出者：Julius Petersen和P.H.Schoute

定理介紹

佩特森-斯豪特定理 如圖1，若△ABC和△A′B′C′是真正相似三角形，並且△AA′A″，△BB′B″和△CC′C″也是真正相似三角形，則△A″B″C″和△ABC也是真正相似三角形。

圖1

佩特森-斯豪特定理與螺旋相似

螺旋相似變換

一個圖形先經伸縮，然後再平移，那么最後得到的圖形和原始圖形的對應直線仍然保持平行，因此結果仍是一個伸縮變換。一般地， 因為同樣的理由，任何兩個伸縮變換的和(即先變換一個，然後再進行另一個伸縮)仍是一個伸縮。另一方面，一個圖形先經伸縮，然後旋轉，那么對應直線就不再保持平行了。這樣，伸縮和旋轉(不是恆等變換或半轉)的和，雖然仍是一個直接相似變換，保持角度的大小和符號，但已不再是一個伸縮變換了。

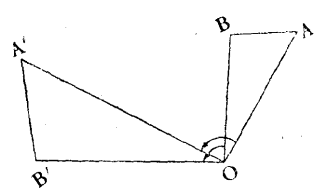圖2

關於同一個中心的伸縮變換與旋轉變換的和，稱為伸縮旋轉變換或螺旋相似變換。對於這種變換人們知道的不多，但在許多問題的求解中用處很大。

如圖2所示，中心為O的螺旋相似，將AB變為A'B'，則△OA'B'和△OAB為直接相似的且∠AOA'=∠BOB'，而且和單單一個伸縮變換的情況一樣，伸縮比為k=OA'/OA= A'B’/AB。

因為任何一個螺旋相似變換被它的中心O，比k和旋轉角度θ所決定，所以我們以符號O(k，θ)表示它(通常逆時針旋轉為正，順時針旋轉為負) 。特別，O(k，0°)和O(k，180°)為圖3和4所分別表示的伸縮變換，而O(1，θ)為一旋轉。

相關定理

作為螺旋相似變換套用的例子，我們來證明

定理1 如果在△ABC的三邊BC、CA、AB上向外作正方形，其中心為O₁、O₂ 、O₃，則線段O₁O₂和CO₃相等且互相垂直。

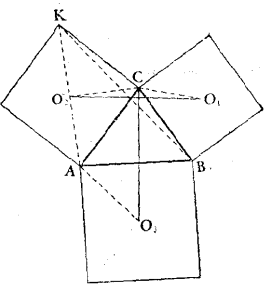圖5

在圖5中，螺旋相似 將△CAO₃，變為△KAB，螺旋相似 將△O₁CO₂變為△BCK。

因為在這兩個變換的像中BK是公共邊，它分別是由O₃C和O₁O₂變來的，而在這兩個變換中伸縮比又是相同的，因此原始三角形的這條邊必定相等，又因O₃C和O₁O₂經過旋轉45°和-45°後的像之間的夾角為0°，所以這兩條線開始時一定互相垂直。

證明到此完畢(注意: AO₁、BO₂、CO₃三條直線是△O₁O₂O₃的高， 因而是共點的)。

在定義螺旋相似為有相同中心的中心伸縮變換和旋轉變換的和以後，我們自然會想到中心不相同的伸縮變換與旋轉變換的和是什麼?答案既簡單又使人感到吃驚——還是一螺旋相似變換，因此不存在更複雜的直接相似變換了。

定理2 任何兩個直接相似圖形由一個平移或一個螺旋相似變換相聯繫。

要證明此，考慮直接相似圖形的兩條對應線段AB和A'B'。如果AB和A'B'平行且長度相等，則變換就是一個平移。要說明這一點，設C為AB外的任何一點，C'為它的像，則由圖形的直接相似性，可以斷言△ABC和△A'B'C'全等，它們的對應邊平行。這樣把任何點和它們的像相連的線段都互相平行且相等，所以這個變換就是一個平移。

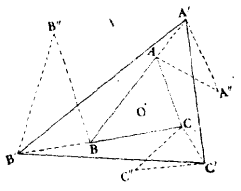圖6

其次，設AB和A'B'長度不等(如果A、B、A'、 B'四點不形成四邊形，那么取一對新的對應線段並取名為AB和A'B'。例如，如果B位於AA'上(如圖6所示)，用AB的中點來代替A，A'B' 的中點代替A')，則如圖7所示，直線AA'和BB'相交於D點。圓ABD和A'B'D有一個公共點D，設另一個公共點為O(或者，如果它們相切於D點，那么設D點另一個名稱為O)，比較角度OAB、ODB、ODB'和OA'B'，我們可知∠OAB=∠OA'B'。同理，∠OBA= ∠OB'A'。這樣，直接相似的△OAB和△OA'B'由一螺旋相似變換O(k,θ)所聯繫，其中k=OA'/OA且θ=∠AOA'。

換言之，不是平移的各個直接相似變換都有一個不動點，而且這個不動點是唯一的。因為如果有兩個不動點，例如說是A和B，那么會產生一條不動的線段AB，因為k=AB/AB=1，所以這個相似變換就是保持兩點固定的等距變換。如果這個變換把△ABC變為△ABC'，我們能把C'安於中心在A和B，半徑為AC和BC的兩個圓上。這樣，保持A和B不變的等距變換隻可能是恆等變換(平移距離為零的平移變換)和反射變換(它不是直接相似的，因為它改變了角的符號)。

例如，把具有不同比例尺的同一個州的兩幅地圖重疊在描跡紙上，那么剛好有一個地方在兩張圖，上用同一點表示(“重疊”一詞是指小比例尺的圖安放於大比例尺的圖內，這時，容易證明螺旋相似的中心為州內一點)。

這個想法曾由彼德森(Julius Petersen)(1880)和紹特(P.H.Schoute)(1890)發展成一個極其美妙的定理，下面是它的一個特殊情況：

佩特森-斯豪特定理特殊情況

定理3 如果△ABC和△A'B'C'是兩個直接相似三角形，而△AA'A"，△BB'B"和△CC'C"為三個直接相似三角形，那么△A”B"C"直接相似於△ABC。

如果△ABC和△A'B'C'經一個平移而全等，那么這個定理是顯然成立的。如果不是平移，那么設O(k,θ)為將△ABC變為△A'B'C'的唯一的螺旋相似變換，則有

k=OA'/OA=OB'/OB=OC'/OC，θ=∠AOA'=∠BOB'=∠COC'(圖6)，

那么有△OAA'∽△0BB'∽△OCC'，

但我們假設有△AA'A"∽△BB'B"∽△CC'C"，

因此△OAA"∽△OBB"∽△OCC"

且:OA"/OA=OB"/OB=OC"/OC=k'，

∠AOA"=∠BOB"=∠COC"=θ' 存在

一個螺旋相似變換O(k',θ')，把△ABC和△A" B"C”相聯。

用同樣方法證明的彼德森-紹特(Petersen-Schoute)定理的另一 種特殊形式為:

定理4 當線段AB.上的所有點P，經一相似變換和A'B'上的P'點相聯時，線段PP’的定比分點或者兩兩不同而在同一條直線上或者全部重合。