基本介紹
- 中文名:低密度同位元檢查累積碼
- 外文名:Low density parity check accumulative code
- 領域:編碼理論
- 組成:低密度奇偶檢查碼、累加器
- 特點:降低編碼難度
- 套用:編碼錯誤檢測與校正
簡介,低密度奇偶檢查碼,累加器,信道編碼,
簡介
低密度同位元檢查累積碼是一種信道編碼方法,低密度同位元檢查累積碼有三個階段。第一個階段是一個可逆線性轉換矩陣,其中有資料來源序列。 第二個階段是一個一個rate的累加器,可以轉換長度為L的序列。第三個階段是變更或置換這個序列。 這個序列接下來會傳送到解碼器,總共需要傳送的碼數量由解碼器的回饋決定。低密度同位元檢查累積碼可以套用在許多編解碼套用的系統當中。
低密度奇偶檢查碼
低密度奇偶檢查碼(Low-density parity-check code,LDPC code),是線性分組碼(linear block code)的一種,用於更正傳輸過程中發生錯誤的編碼方式。在1962年,低密度奇偶檢查碼(LDPC code)即被Gallager提出,並被證明其錯誤校正能力非常接近理論最大值,香農極限(Shannon Limit);不過受限於當時技術,低密度奇偶檢查碼並無法實現。低密度奇偶檢查碼被重新發現,並隨著積體電路的技術演進,低密度奇偶檢查碼的實現逐漸可行,而成為各種先進通信系統的頻道編碼標準。
低密度奇偶檢查碼是基於具有稀疏矩陣性質的奇偶檢驗矩陣建構而成。對(n, k)的低密度奇偶檢查碼而言,每k比特數據會使用n比特的碼字(codeword)編碼。以下是一個被(16, 8)的低密度奇偶檢查碼使用的奇偶檢驗矩陣H。當中可以見得矩陣內的元素1數量遠少於元素0數量,所以具有稀疏矩陣性質,也就是低密度的由來。

低密度奇偶檢查碼的解碼,可對應成二分圖(bipartite graph)作表示。下方的二分圖是依照上述奇偶檢驗矩陣H建置,其中H的行(column)對應至check node,而H的列(row)對應至bit node。check node和bit node之間的連線,由H內的元素1決定;好比H中第一行(column)和第一列(row)的元素1,使check node和bitnode兩者各自最左手邊的第一個彼此連線。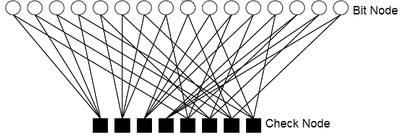 二分圖
二分圖
 二分圖
二分圖低密度奇偶檢查碼的解碼算法,主要基於有疊代性(iterative)的置信傳播(belief propagation);整個解碼流程如下方所示:
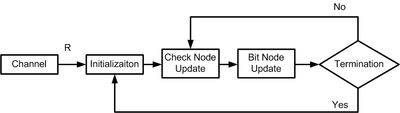 解碼流程圖
解碼流程圖- 當接收數據R從通信頻道(channel)進入低密度奇偶檢查碼的解碼器,解碼器會對訊息作初始化(initialization)。
- check node根據互相連線的多個bit node內的數據做更新運算(update)。
- bit node對相連線的多個check node內的數據做更新運算。
- 觀察終止(termination)條件,來決定是否繼續疊代計算。
累加器
在中央處理器中,累加器 (accumulator) 是一種暫存器,用來儲存計算產生的中間結果(在運算器中,形成和存放運算 結果的暫存器);或指可以存儲一數並接受另一數,將兩者相 加後存儲其總和的設備稱累加器。累加器還 具有移位、讀出信號、清除、求補等功能。
如果沒有像累加器這樣的暫存器,那么在每次計算 (加法,乘法,移位等等) 後就必須要把結果寫回到 記憶體,也許馬上就得讀回來。然而存取主存的速度是比從算術邏輯單元到有直接路徑的累加器存取更慢。標準的例子就是把一列的數字加起來。一開始累加器設定為零,每個數字依序地被加到累加器中,當所有的數字都被加入後,結果才寫回到主存中。
信道編碼
一種為了提高通信系統可靠性而對傳輸信號進行的編碼。即使所傳輸信號內部具有更強的規律性和相關性,以使信號受干擾而損傷時仍能正確恢復原有信息的處理過程。即為了適應信道條件(如頻頻寬度限制、波段、功率、通信時間等)和滿足通信的要求(如可靠性、有效性等),需要對所傳輸的信號進行的某種變換。信道編碼的理論基礎是資訊理論中的信道編碼定理,它從理論上解決理想編碼器的存在性問題。信道編碼的具體方法屬於差錯控制技術。
能檢出和糾正傳輸中產生錯誤的編碼。用於檢錯的碼叫檢錯碼;用於檢錯與糾錯相結合的碼稱為“糾錯碼”。按糾錯類型可分糾隨機錯誤碼、糾突發錯誤碼,糾位元組(byte)錯誤碼和糾運算錯誤的算術運算碼等。按構造可分分組碼和樹碼。分組碼是將M個符號序列分別映射成長度為n的碼字。如該映射規律滿足線性關係,則稱為“線性碼”,否則稱為“非線性碼”。樹碼具有樹形結構,可用樹形圖描述。狀態有限的樹圖可簡併成格狀圖,稱為格狀碼。由分組碼和樹碼級連的碼稱為“級連碼”,它具有更強的糾錯性能並更易於實現。糾錯碼的糾錯能力和有效的解碼算法是研究信道編碼的焦點。Turbo碼和低密度奇偶校驗(LDPC)碼是兩種性能逼近仙農限的最令人矚目的糾錯碼。信道編碼已在各類數字通信系統中得到廣泛套用。其發展趨勢是調製與糾錯相結合,信道編碼與信源編碼相結合等。