伊藤積分公式(CItoformula)隨機積分理論的一個重要公式.設F(二,,二:,...,xn;y
y}
...,y;)為}n+“上的函式,關於每個二,一次連續可微,關於每個y*二次連續可微.令X川,Xcz},.,,Xc.},',為n個適應有限變差過程,}rcl),}r(z),…,}r(rn,'',’為m個半鞅,則
上面的伊藤積分公式是隨機積分理論中一個最重要的結果,它給出了半鞅的複合函式的一個微分法則.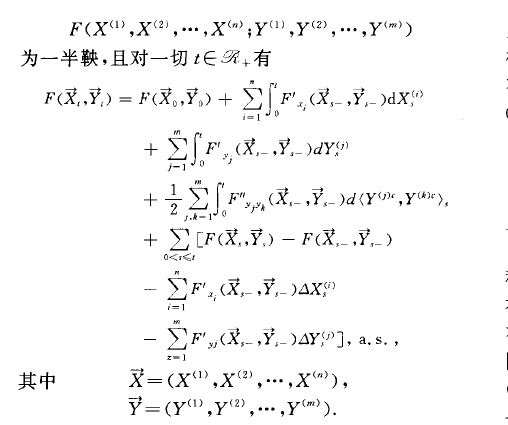
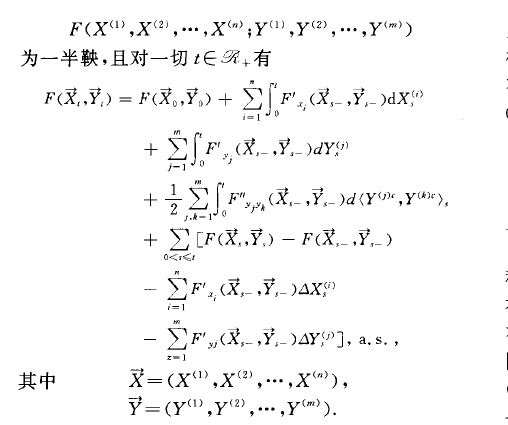
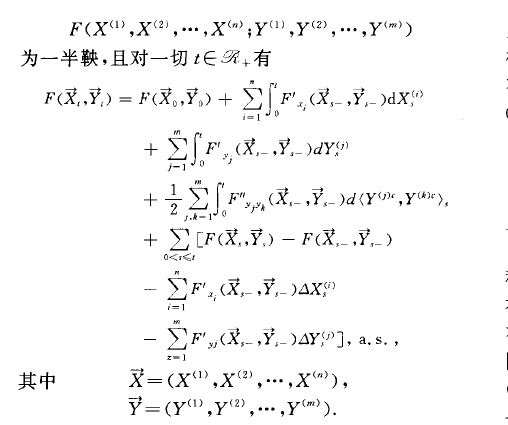
伊藤積分公式(CItoformula)隨機積分理論的一個重要公式.設F(二,,二:,...,xn;y y} ...,y;)為}n+“上的函式,關於每個二,一次連續可微,關於每個y*二次...
伊藤積分最重要的性質是著名的伊藤公式:設F是二次連續可微的實函式,則這一公式及其各種推廣在理論上和套用上都有重要的作用。例如, 可以用來證明關於布朗運動的鞅...
的斯特拉托諾維奇積分。這 時對(關)的限制要比伊藤積分情形強得多. 斯特拉托諾維奇積分確定的不再是鞅或局部鞅 了.但它的微分法則與通常的微積分相似而不像伊 藤...
積分或隨機分析這個新分支,1951年他引進計算隨機積分的伊藤公式,後推廣成一般的變元替換公式,這是隨機分析的基礎定理.同時他定義多重Wiener積分和復多重Wiener積分。...
