在一般的更新過程中,只考慮系統只有一個狀態的情況,比如,機器一直是開的(即更新零件不需要時間).而實際上,零件損壞後會有一個拆卸更換的過程,這段時間機器是“關”的.這樣有“開”和“關”兩種狀態的更新過程稱為交替更新過程。
基本介紹
- 中文名:交替更新過程
- 外文名:alternating renewal process
- 所屬領域:數理科學
- 研究對象:隨機變數
- 性質:機率事件
相關重要結論,詳解,
相關重要結論
設系統最初是開的,持續開的時間是Z1,而後關閉,時間為Y1之後再打開,時間為Z2又關閉,時間為Y2,...交替進行,每當系統被打開稱作一次更新.
我們假設隨機向量列{(Zn,Yn),n≥1}是獨立同分布的,從而{Zn),{Yn}都是獨立同分布的,即Zi,Yi在i≠j時獨立,但Zi,Yi允許不獨立.
下面利用關鍵更新定理得到交替更新過程的一個很重要的結論.
定理:設H是Zn的分布,G是Yn的分布,F是Zn+Yn的分布.並記P(t)=P{t時刻系統是開的),設E(Yn+Zn)<∞,且F不是格點的,則
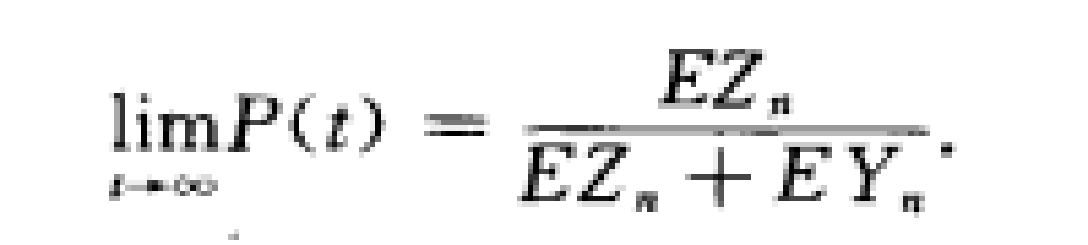
證明 : 對第一次更新的時刻X1=Z1+Y1,取條件機率得:

則:

方程解為:
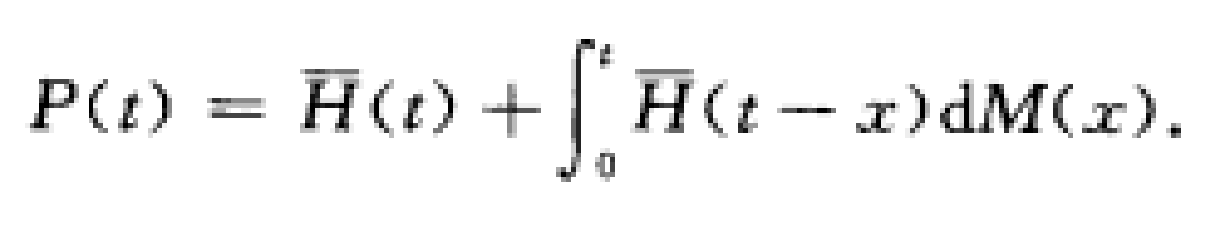
又:

且顯然 非負不增,由關鍵更新定理得:
非負不增,由關鍵更新定理得:

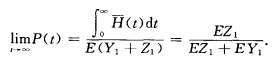
詳解
考慮較一般的情形,即當零件失效時,用新零件更替用壞的零件需要一定的時間(一般說來,這段時間的長度是隨機的)去尋找、拆卸損壞的零件和安裝新零件。於是對應的系統就有兩種狀態——工作狀態和故障(或者說修理)狀態。這時就需要用一個兩狀態(通常記為狀態“1”和“0”)的隨機過程來描述設備的工作情況。該過程交替地取值“1”和“0”,即設備交替地處於工作和故障狀態。由此引導到如下的交替更新過程模型。
系統有“1”和“0”兩種狀態。假設在初始時刻系統處於狀態“1”,在該狀態逗留一段時間Z1後轉移到狀態“0”,在“0”的逗留時間是Y1,接著它又轉回狀態“1”並在“1”逗留長為Z2的時間,以後又轉到狀態“0”,在該狀態度過長為Y2的時間後又轉回“1”,…如此相繼在狀態“l”和“0”之間交替轉移下去。由於系統在這兩個狀態的逗留時間是隨機的,我們就得到兩串隨機變數Z1,Z2,…,Zn,…和Y1,Y2,…,Yn,…進一步假設(Z1,Y1),(Z2,Y2),…,(Zn,Yn),…是相互獨立同分布的,但對任一固定的n,Zn和Yn可以相依。由對{(Zn,Yn)}所加條件知{Zn)和{Yn}各自都是相互獨立同分布的隨機變數序列。我們把由隨機向量序列{(Zn,Yn)}確定的隨機過程(或該序列自身)稱做交替更新過程。
顯然,若Yn=0對所有n,則由{(Zn,Yn)}描述的交替更新過程就變為由{Zn}描述的普通更新過程。
從上面對交替更新過程的描述可以看出,系統每一次從狀態“0”轉移到狀態“1”的時刻是過程的一個“再生點”。這就是說,從機率分布律的觀點看,過程從該時刻開始往後的發展如同過程從頭開始一樣(而不受過程在該時刻以前的歷史影響)。易見普通更新過程的每一個更新時刻都是過程的再生點。再生點這一概念在套用機率中很重要。
令H,G和F分別表示Zn,Yn和Zn+Yn(n==1,2.··)的分布。又記
P1(t)=P(在時刻t系統處於狀態“1”),
P0(t)=P(在時刻t系統處於狀態“0”)。
下面的定理在排隊論和可靠性理論中很有用。
定理1 設E(Zn+Yn)<∞,F是非格子分布,則

定理2 若Zn和Yn相互獨立,Zn和Yn的分布H和G分別有密度函式h和g,則
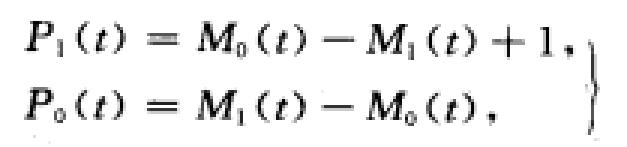
式中Mi(t)=ENi(t)(i=0,1),而Ni(t)則是過程在區間(o,t]中狀態“i”的更新次數,即從狀態“i”轉移到另一狀態的次數。

