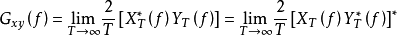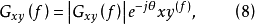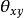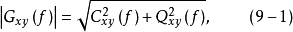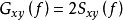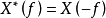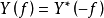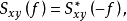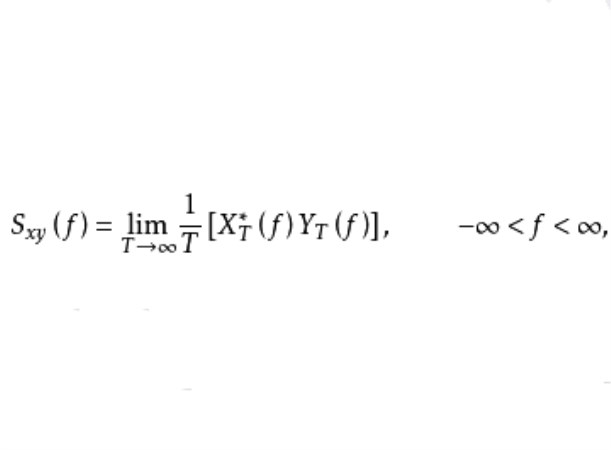互譜密度函式

互譜密度函式(cross-spectral density function)是互相關函式的傅立葉變換。互譜密度函式一般與互相關函式具有同樣的套用，但它提供的結果是頻率的函式而不是時間的函式。這—事實大大開拓了使用範圍，因此在可以套用相關分析的工程問題中大大增加了互譜方法的套用。互譜密度函式是有重要用途的，頻譜分析中能用互譜的測量結果來識別動力系統的特性以及計算頻響函式的振幅比和相位角。

基本介紹

• 中文名：互譜密度函式
• 外文名：cross-spectral density function
• 所屬學科：數理科學
• 簡介：互相關函式的傅立葉變換

互譜密度函式的定義

互譜密度函式的定義，數學上可描述為

由於互譜密度函式的推導方法與自譜密度函式相同，它們的差別只是是信號x(t)的自乘，而是信號與的互乘。應當注意的是，因為與一般不是互為共軛，所以為複數性質。

互譜的單邊譜為

由式(2)互譜密度函式也可以描述為

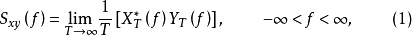
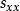
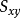
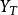
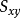
互譜密度函式的性質

1．的數學屬性

因為一般與是複數且不是互為共軛，所以為複數性質。

2．的共軛變數交換性

證明：

式中：下標表示兩個測量信號的隨機變數x、y，該式表明，數值上等於兩個信號x、y的信道互相交換後其應對的互譜密度函式取共軛的結果。

3．互譜密度函式與互相關函式的關係

與關係類似，可以得到也是一個傅立葉變換對，即有

4．互譜密度函式的振幅和相位

1)共譜密度函式和重譜密度函式

由互譜密度函式與互相關函式的關係得

其中：共譜密度函式為實部，重譜密度函式為虛部。有

2)互譜密度函式的振幅和相位

由式(5)、式(6)和式(7)，可把互譜密度函式寫成複數表示式，有

式中：和分別為互譜密度函式的振幅和相位，有

振幅：

相位：

3)相位的含義

由時域中的時延將引起頻域中的相移，可推斷出的含義：為反映信號y(t)相對信號x(t)時延方面的信息，為正，意味著在頻率處信號y(t)落後於信號x(t)，反之亦然。

5．的證明

由傅立葉譜關於f=o軸共軛對稱的性質，有和，將它們的左邊和右邊分別相乘後，得

再將互譜密度函式的共軛變數交換性代入上式，得

由此看出，與一樣，也具有關於f=0軸共軛對稱的性質。根據互譜密度函式的振幅為取摸概念，對於雙邊譜的振幅有

取摸後為關於f=0軸對稱，所以互譜的單邊譜可描述為

互譜的單邊譜為複數性質，也可描述為。