二階退化雙曲型方程(degenerate hyperbolic equation of second order)是一類重要的特殊的雙曲型方程。如果研究的二階偏微分方程的特徵形式,在所考慮的區域的每一點上有一個負特徵值而其餘特徵值為正或零,則這類二階偏微分方程稱為退化雙曲型方程。
基本介紹
- 中文名:二階退化雙曲型方程
- 外文名:degenerate hyperbolic equation of second order
- 領域:數學
- 學科:微分方程
- 性質:一類重要的特殊的雙曲型方程
- 本質:二階偏微分方程
概念,雙曲型方程,偏微分方程,特徵方程,微分方程,
概念
二階退化雙曲型方程(degenerate hyperbolic equation of second order)是一類重要的特殊的雙曲型方程。如果研究的二階偏微分方程的特徵形式,在所考慮的區域的每一點上有一個負特徵值而其餘特徵值為正或零,則這類二階偏微分方程稱為退化雙曲型方程。有時也稱為弱雙曲型方程。它可以用研究具非負特徵形式的方程的方法進行研究。
雙曲型方程
雙曲型偏微分方程是描述振動或波動現象的一類重要的偏微分方程。雙曲型偏微分方程解可以分解為振動與振動相乘,或指數函式與指數函式相乘的形式,一般能量無窮。
雙曲型偏微分方程簡稱雙曲型方程,是偏微分方程的一種類型。它主要用於描述振動、波動現象與相應的運動過程。它的一個典型特例是波動方程和n=1時的波動方程。可用來描述弦的微小橫振動,稱為弦振動方程。這是最早得到系統研究的一個偏微分方程。
雙曲型方程最重要的性質是其柯西問題的適定性。有時人們也用此來作為雙曲型方程定義的基礎。對於非線性雙曲型方程,雙曲型的定義一般要依賴於所考察方程的解。非線性雙曲型方程柯西問題光滑的存在性一般只能是局部的。它的解在有限時間內會產生奇性。
偏微分方程
含有未知函式的偏導數的方程稱為偏微分方程,是微分方程的分支。含於方程中的偏導數的最高階稱方程的 階。例如,
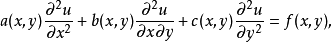
二階線性與非線性偏微分方程始終是重要的研究對象。這類方程通常劃分成橢圓型、雙曲型與拋物型 三類,圍繞這三類方程所建立和討論的基本問題是各 種邊值問題、初值問題與混合問題之解的存在性、唯 一性、穩定性及漸近性等性質以及求解方法。近代物理學、力學及工程技術的發展產生出許多新的非線性問題,它們常常導引出除上述方程之外的稱為混合型方程、退化型方程及高階偏微分方程等有關問題,這些問題通常十分複雜具有較大的難度,至今為止,一 直是重要的研究課題。對於偏微分方程問題的討論和 解決,往往需要套用泛函分析、代數與拓撲學、微分幾何學等其它數學分支的理論和方法。另一方面,由於電子計算機的迅速發展,使得各種方程均可數值求解,並且揭示了許多重要事實,因此,數值解法的研究,在已取得許多重要成果的基礎上,將會有更快地發展。
特徵方程
特徵方程是為研究相應的數學對象而引入的一些等式,它因數學對象不同而不同,包括數列特徵方程、矩陣特徵方程、微分方程特徵方程、積分方程特徵方程等等。
遞推是中學數學中一個非常重要的概念和方法,遞推數列問題能力要求高,內在聯繫密切,蘊含著不少精妙的數學思想和數學方法。新教材將數列放在高一講授,並明確給出“遞推公式”的概念:如果已知數列 的第1項(或前幾項),且任一項 與它的前一項 (或前幾項)間的關係可以用一個公式來表示,那么這個公式叫做數列的遞推公式。有通項公式的數列只是少數,研究遞推數列公式給出數列的方法可使我們研究數列的範圍大大擴展。新大綱關於遞推數列規定的教學目標是“了解遞推公式是給出數列的一種方法,並能根據遞推公式寫出數列的前幾項”,但從近十年來高考試題中常以遞推數列或與其相關的問題作為能力型試題來看,這一目標是否恰當似乎值得探討,筆者以為“根據遞推公式寫出數列的前幾項”無論從思想方法還是從培養能力上來看,都不那么重要,重要的是學會如何去發現數列的遞推關係,學會如何將遞推關係轉化為數列的通項公式的方法。
微分方程
表示未知函式及其導數與自變數或微分之間的關係的方程。如果未知函式是一元函式,則稱之為常微分方程;如果未知函式是多元函式,方程中含偏導數則稱之為偏微分方程。
微分方程中出現的未知函式的導數的最高階數稱為微分方程的階。
如果微分方程關於未知函式及其導數是線性的就稱之為線性微分方程;不是線性的,就稱為之非線性微分方程。
使微分方程成為恆等式的函式稱為微分方程的解。含任意常數且獨立任意常數的個數等於微分方程的階數的解稱為微分方程的通解;任意常數取特定值的解稱為微分方程的特解,由通解確定任意常數特定值的給定條件叫初始條件。
