二進神經網路

二進神經網路(Binaiy Neural Networks)，二進前向神經網路的簡稱，是輸入與輸出均為二進制的一種人工神經網路，可以精確實現任意給定的布爾函式。二進神經網路主要採用輸入、隱層、輸出三層結構，神經元採用硬限幅函式作為激發函式，每個神經元等價於一個分類超平面。

基本介紹

• 中文名：二進神經網路
• 外文名：binary neural networks
• 全稱：二進制前向神經網路
• 釋義：輸入輸出均為二進制的神經網路
• 套用：模式識別、人工智慧等
• 主要研究內容：知識提取、分類能力、學習算法

簡介

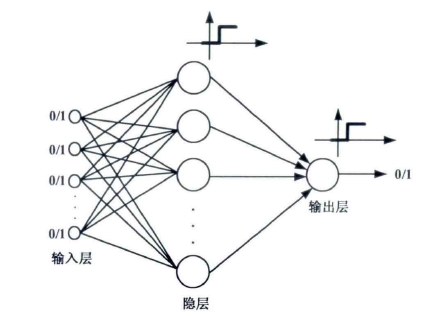
二進神經網路是指具有以下三個特性的網路：(1)只有單隱層和單輸出；(2)網路各個神經元均為硬限幅特性神經元；(3)網路的輸入、輸出均為二進制，即0和1。稱每個神經元為二進神經元。

二進前向神經網路處理的信息對象是定義在二進制空間的變數，由於二進制變數形式簡單，較易得到處理，並且任何變數在一定的量化精度下都可以轉換為二進制變數，二進制函式具有直接的邏輯意義，因此二進神經網路中蘊含的知識在結構上相對較易分析，具有普適性。

二進神經網路的套用範圍主要集中在模式識別、人工智慧、大規模積體電路設計，複雜邏輯綜合等方面,

二進神經網路模型

神經元的數學模型

人工神經元的結構模型如圖1所示。 為輸入信號， 為神經元內部狀態， 為閾值， 為 到 的連線權， 表示外部輸入信號(在某些情況下，它可以控制神經元 ，使 可以保持在某一狀態)， 為激發函式， 為輸出，上述模型可以描述為：

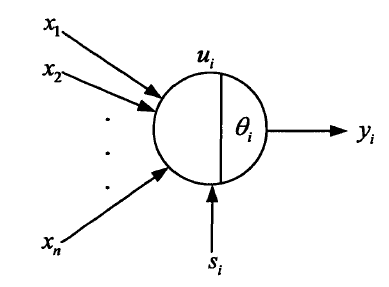
圖1 神經元的結構模型

其中， 。

當神經元沒有內部狀態時，可令 ， 。通常的情況是沒有外部信號 的，此時每個神經元的輸入只接受前一級神經元的輸出，因此，對神經元i的總作用 為所有的加權和減去閾值，此作用引起神經元i的狀態變化，而神經元的輸出 為其當前狀態 的函式。

二進前向神經網路結構

前向網路統指只有信息從輸入到輸出單方向流動的人工神經網路，如多層前饋網路、徑向基函式網路等。其中，多層前饋網路是最為典型的一種，也稱為前向網路(或多層感知器)。這種前向網路是指：

(1)網路中神經元是分層的，每一層有一個或多個神經元；每一層中的神經元輸出僅在同其下一層相鄰的神經元的輸入相連線，而與其自身或其它層神經元無任何連線。

(2)神經元的模型如圖1所示。其中單個神經元的輸入輸出關係表示為： ，這裡 為該神經元的激發函式。

(3)神經元的激發函式 通常有兩類：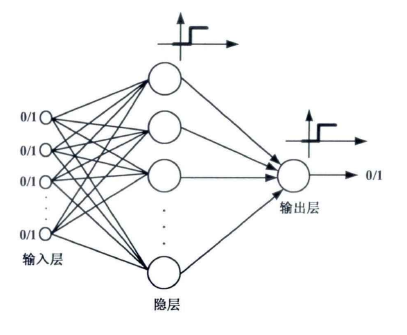

圖2 二進前向神經網路

硬限幅函式(Hard-Limitation)： ；

軟限幅函式(Sigmoid)： ，其中， 為表示這一單調變化函式變化速度的參數。

通常也把前向網路中的神經元稱為感知器。

若二進神經網路中有n個輸入，H個隱層神經元，則記為n-h-1，其結構如圖2所示。

主要研究內容

二進神經網路的研究是神經網路研究的一個分支，主要的研究內容包括二進神經網路的知識提取、二進神經網路的分類能力和二進神經網路學習算法。

二進神經網路的知識提取

神經網路主要的缺點是獲得的知識隱含在網路的一系列連線權中，處理過程無法為用戶所了解，缺乏透明性，使得套用受到限制，故需建立一個解釋機制，用規則代替權值矩陣。

由於二進神經網路的特殊性，每個二進神經元都等價於一個線性可分函式，但對於每個神經元所表達線性可分函式的邏輯意義仍不完全清楚，僅對二進神經元所對應的某些線性可分結構系有明確等價判別法及邏輯意義;如果任意一個二進神經元都對應於一種有明確邏輯意義的線性可分結構，則對於二進神經網路的知識提取將變得容易;另外，對於非線性可分函式也可以有目標地分解為幾類線性可分結構系之間的邏輯運算，因而對於二進神經網路中線性可分結構系的研究有著重要意義。

二進神經網路的分類能力

神經網路的基本功能之一是分類，而神經網路的分類能力是指對於同樣的分類問題，要達到同樣的分類效果，網路所需神經元的數目越少，網路的分類能力越強，網路的結構越簡單，其分類能力也越強。由於二進神經網路中每個神經元等價於一個線性可分函式，故分析每個神經元的分類能力有助於分析網路的非線性可分能力。

二進神經網路的學習算法

神經網路的基本功能之二是函式逼近，而二進神經網路主要用來實現布爾函式。神經網路分類能力尚未完全了解，也即不能確定網路中隱層神經元所需的最小數目，故對於給定的布爾函式，需設計算法使得採用簡潔的網路結構來實現。另外對於學習算法的研究，對於一些特殊的布爾函式(如奇偶校驗問題)，隱層神經元數目也可以有進一步的了解。

二進神經網路知識提取的主要方法

KT方法

KT方法是LiMiu Fu於1994年提出的蘊含性規則提取方法，KT方法是對採用閾函式的二進神經網路的完備規則提取方法，並且它適用於任何學習算法的結果。雖然KT方法是完備的，但也存在一些弱點，主要體現在：KT方法採用蘊含性規則，既使對A∧B這樣的簡單邏輯,要想完備表達也要至少3條規則。對於一些較為複雜的邏輯，提取出的規則更多，特別是它不能表達出某些二進神經元最本質的邏輯內涵，漢明球就是一個例子，如果用KT方法對漢明球這種線性可分的空間結構進行分析，結果十分複雜。

MofN方法

MofN方法是Towell G G和Sharlik J W於1993年提出的規則提取方法，MofN規則提取方法在規則表達形式上十分獨特，在某些情況下比KT方法能更清晰地接近於邏輯的本質，但是也並不是任何一個二進神經元都是可以用MofN方法簡明清晰表達的，因此，通常情況下MofN方法和KT方法都有各自相對較適用的範圍，對於任意的二進神經網路學習算法的學習結果，需要具體分析。

CH判據

CH判據是我國學者程輝於1993年提出的，它在研究二進神經網路權係數、閾值和所表達的邏輯規則的關係問題上，比KT方法更量化，也更本質化，但是CH判據僅僅解決了二進制空間中正超立方體，凹超立方體和凸超立方體這幾類線性可分結構的構造問題。如果想用CH判據進行規則提取，就要求神經網路的最終學習結果要滿足CH判據對權係數的約束要求，這一點造成了對二進神經網路學習算法的特殊要求，從而使這種方法的套用受到局。

漢明聚類法

漢明聚類法(HC)是由Marco Muselli於1959年提出的一種知識提取法，這種方法以正超立方體為每個二進神經元的基本線性可分結構，輸出元採用或邏輯。正超立方體是最簡單的與邏輯內涵，所以這種方法對規則的表達效率僅僅類似於用卡諾圖化簡邏輯函式，在知識的表達效率和對其它學習算法結果的適應性方面存在很大局限性。