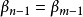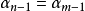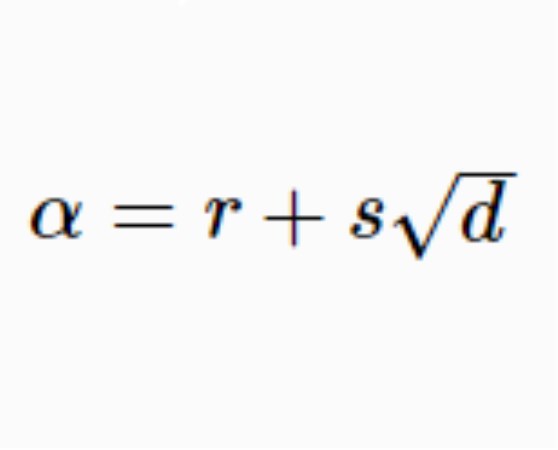基本介紹
- 中文名:二次無理數
- 外文名:quadratic irrational number
- 所屬學科:數學
- 所屬問題:初等數論(連分數)
- 簡介:滿足整係數二次方程的無理數
基本概念,相關定理及概念,
基本概念
定義 一個複數α稱為二次無理數,如果它是某個整係數二次方程
ax2+bx+c=0
的根。特別地,當二次無理數α是實數時,我們就稱其為實二次無理數。任何無限循環連分數表示二次無理數,任何二次無理數都可用無限循環連分數來表示。
相關定理及概念
定理1α是二次無理數的充分必要條件是存在非平方的整數d,及有理數r,s,s≠0,使
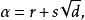
定理2 設整數d不是平方數,那么形如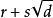 (r,s是有理數)的數的和、差、積、商仍然是這種形式。
(r,s是有理數)的數的和、差、積、商仍然是這種形式。
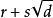
定義 對於無限簡單連分數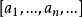 ,如果存在兩個整數s≥0,t>0使得
,如果存在兩個整數s≥0,t>0使得
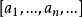
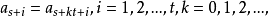
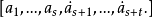
例如a=[5,3,4,1,2,1,2,…],則這個循環連分數的s=3,t=2。
定理3 一個循環連分數必是實二次無理數,即是某個整係數二次不可約方程的根。反之亦然。
每個純循環連分數收斂於一個二次無理數α,滿足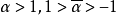 ,下面是其逆命題。
,下面是其逆命題。
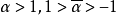
設α是一個二次無理數,滿足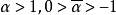 ,存在正整數p,q,d,其中d是非平方數,使得p
,存在正整數p,q,d,其中d是非平方數,使得p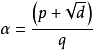 。
。
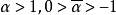
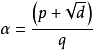
2.設d是非平方正整數,p和q是整數,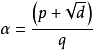 ,
,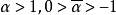 ,則:
,則:
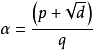
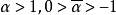
(1)若 ,其中
,其中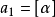 ,其中
,其中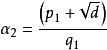 ,其中
,其中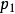 和
和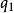 是整數;
是整數;

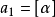
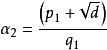
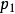
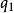
(2)若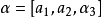 ,其中
,其中 ,則
,則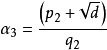 ,其中p2和q2是整數;
,其中p2和q2是整數;
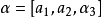

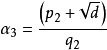
(3)若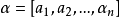 ,其中
,其中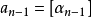 ,則
,則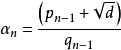 ,其中
,其中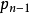 與
與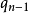 是整數;
是整數;
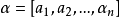
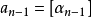
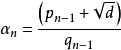
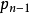
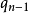
(4)每個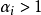 且
且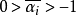 ;
;
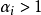
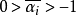
(5)只有有限多個不同的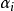 ;
;
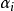
(6)若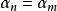 (1≤n≤m)是第一次重複出現的兩個數,則
(1≤n≤m)是第一次重複出現的兩個數,則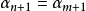 ,進而利用歸納法得到
,進而利用歸納法得到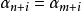 對一切正整數i成立;
對一切正整數i成立;
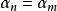
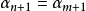
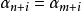
(7)若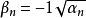 ,則對一切n有
,則對一切n有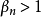 ;
;
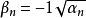
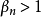
(8)若n>1,則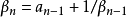 ,所以
,所以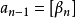 ;
;
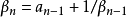
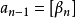
(9)因為 ,所以
,所以 ,且
,且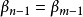 ,於是
,於是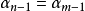 ,因此n=1。
,因此n=1。