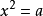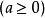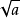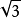平方根,又叫二次方根,表示為〔±√ ̄〕,其中屬於非負數的平方根稱之為算術平方根(arithmetic square root)。一個正數有兩個實平方根,它們互為相反數,負數沒有平方根
基本介紹
- 中文名:平方根
- 外文名:Square root
- 所屬學科:數學
- 別名:二次方根
- 分類:數學代數類
公式,運算,描述,過程1,過程2,過程3,例子,牛頓疊代法,知識教案,
公式
結論:被開方數越大,對應的算術平方根也越大(對所有正數都成立)。
負數在實數系內不能開平方。只有在複數系內,負數才可以開平方。負數的平方根為一對共軛純虛數。例如:-1的平方根為±i,-9的平方根為±3i,其中i為虛數單位。規定: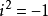 ,或
,或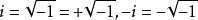 。一般地,“√ ̄”僅用來表示算術平方根,即非負數的非負平方根。
。一般地,“√ ̄”僅用來表示算術平方根,即非負數的非負平方根。
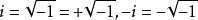
規定:0的算術平方根為0。
運算
描述
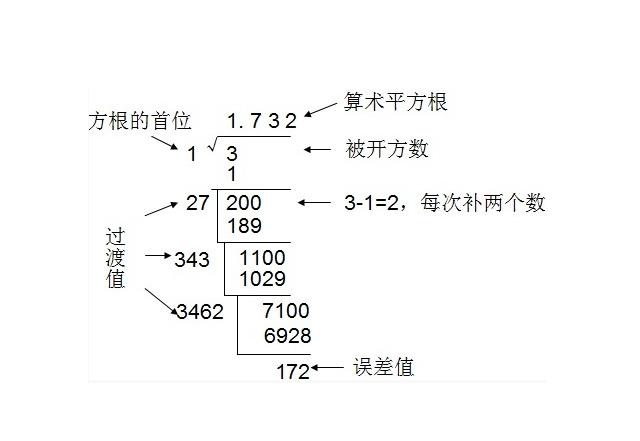
過程1
過程2
每一個過渡數都是由上一個過渡數變化而後,上一個過渡數的個位數乘以2,如果需要進位,則往前面進1,然後個位升十位。以此類推,而個位上補上新的運算數字。簡單地講,過渡數27,是第一次商的1乘以20,把個位上的0用第二次商的7來換,過渡數343是前兩次商的17乘以20=340,其中個位0用第三次商的3來換,第三個過渡數3462是前三次商173乘以20=3460,把個位0用第四次的商2來換,依次類推。
過程3
誤差值的作用。如果要求精確到更高的小數數位,可以按規則,對誤差值繼續進行運算。
例子
計算√10
3. 1 6 2 2 7--------
-----------------------------
√10’00’00’00’00’--------
3| 9 3 第1位3
-------
6 1|100 2*3*10+1 =61 第2位1
| 61
-------
626 | 3900 2*31*10+6 =626 第3位6
| 3756
--------
6322|14400 2*316*10+2 =6322 第4位2
|12644
---------
63242|175600
|126484
-----------
632447|4911600
|4427129
---------
××××××00(如此循環下去)
所以,√10=3.16227…
3. 1 6 2 2 7--------
-----------------------------
√10’00’00’00’00’--------
3| 9 3 第1位3
-------
6 1|100 2*3*10+1 =61 第2位1
| 61
-------
626 | 3900 2*31*10+6 =626 第3位6
| 3756
--------
6322|14400 2*316*10+2 =6322 第4位2
|12644
---------
63242|175600
|126484
-----------
632447|4911600
|4427129
---------
××××××00(如此循環下去)
所以,√10=3.16227…
再如√7
= 2. 6 4 5 …
---------------------
2 | 7
4
--------------
4 6 |300
276
--------------------
52 4 | 2400
2096
-----------------------------
528 5 | 30400
26425
-------------------------------
5290?| 3 9 75 00
---------------------
2 | 7
4
--------------
4 6 |300
276
--------------------
52 4 | 2400
2096
-----------------------------
528 5 | 30400
26425
-------------------------------
5290?| 3 9 75 00
牛頓疊代法
上述筆算開方方法是我們大多數人上學時課本附錄給出的方法,實際中運算中太麻煩了。我們可以採取下面辦法:
比如136161這個數字,首先我們找到一個和136161的平方根比較接近的數,任選一個,比方說300到400間的任何一個數,這裡選350,作為代表。
我們先計算0.5(350+136161/350),結果為369.5。
然後我們再計算0.5(369.5+136161/369.5)得到369.0003,我們發現369.5和369.0003相差無幾,並且3692末尾數字為1。我們有理由斷定3692=136161。
一般來說,能夠開方開的盡的,用上述方法算一兩次基本結果就出來了。再舉個例子:計算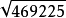 。首先我們發現6002<469225<7002,我們可以挑選650作為第一次計算的數。即算0.5(650+469225/650)得到685.9。而685附近只有6852末尾數字是5,因此6852=469225。從而
。首先我們發現6002<469225<7002,我們可以挑選650作為第一次計算的數。即算0.5(650+469225/650)得到685.9。而685附近只有6852末尾數字是5,因此6852=469225。從而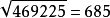 。
。
對於那些開方開不盡的數,用這種方法算兩三次精度就很可觀了,一般達到小數點後好幾位。
實際中這種算法也是計算機用於開方的算法。
我們先計算0.5(350+136161/350),結果為369.5。
然後我們再計算0.5(369.5+136161/369.5)得到369.0003,我們發現369.5和369.0003相差無幾,並且3692末尾數字為1。我們有理由斷定3692=136161。
一般來說,能夠開方開的盡的,用上述方法算一兩次基本結果就出來了。再舉個例子:計算
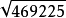
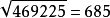
對於那些開方開不盡的數,用這種方法算兩三次精度就很可觀了,一般達到小數點後好幾位。
實際中這種算法也是計算機用於開方的算法。
用Ruby求平方根
(註:sqrt = square root平方根)
module MyMath def sqrt(num,rx=1,e=1e-10) #參數1,需要求平方根的目標;參數2,疊代區間;參數3,精度 num*=1.0 #目標初始化 (num-rx*rx).abs < e ? rx : sqrt(num,(num/rx+rx)/2,e) #計算平方根 endendinclude MyMathputs sqrt(2) #求2的平方根puts sqrt(2,5,0.01) #求2的平方根+疊代區間與精度。
C語言版求平方根
double Sqrt(double a,double p)//a是被開平方根數,p是所求精度{ double x=1.0;double cheak; do { x = (a / x + x) / 2.0; cheak = x * x - a; } while((cheak >= 0 ? cheak : -cheak) > p); return x;}int main(){ printf("%.4f\n",Sqrt(2.0,0.0001)); printf("%.4f\n",Sqrt(0.09,0.0001)); return 0;}輸出結果:
1.4142
0.3000
知識教案
算術平方根定義:
如果一個非負數x的平方等於a,那么這個非負數x叫做a的算術平方根,記作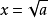 。其中,a叫做被開方數。例如:因為2和-2的平方都是4,且只有2是正數,所以2就是4的算術平方根。
。其中,a叫做被開方數。例如:因為2和-2的平方都是4,且只有2是正數,所以2就是4的算術平方根。
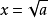
由於正數的平方根互為相反數,因此正數的平方根可分別記作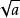 和
和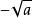 ,可合寫為
,可合寫為 。例如5的平方根可以分別記作
。例如5的平方根可以分別記作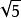 和
和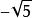 ,可合寫為
,可合寫為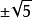 。
。
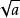
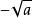

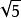
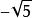
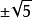
0的平方根僅有一個,就是0本身。而0本身也是非負數,因此0也是0的算術平方根。可記作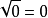 。
。
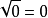
注意:算術平方根只有一個!
教學重點與難點分析
1.本節重點是平方根和算術平方根的概念。平方根是開方運算的基礎,是引入無理數的準備知識。平方根概念的正確理解有助於符號表示的理解,是正確求平方根運算的前提,並且直接影響到二次根式的學習。算術根的教學不但是本章教學的重點,也是今後數學學習的重點。在後面學習的根式運算中,歸根結底是算術根的運算,非算術根也要轉化為算術根。
2.本節難點是平方根與算術平方根的區別與聯繫。首先這兩個概念容易混淆,而且各自的符號表示意義學生不是很容易區分,教學中要抓住算術平方根式平方根中正的那個,講清各自符號的意義,區分兩種表示的不同。
3.本節主要內容是平方根和算術平方根,注意數字要簡單,關鍵讓學生理解概念。另外在文字敘述時注意語言的嚴謹規範。
求平方根教學重點難點
1.教學重點是用計算器求一個正數的平方根的程式,無論實際生活,還是其他學科都會經常用到計算器求一個數的平方根,這也是學生的基本技能之一。
3.在給學生講解如何利用計算器求一個數的平方根時,應掌握方法。