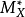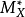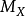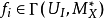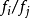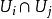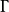主除子(principal divisor)域中一個元素決定的除子,主理想概念的推廣。如果兩個卡吉耶除子相差一個主除子,則兩個卡吉耶除子稱為是線性等價的。
基本介紹
- 中文名:主除子
- 外文名:principal divisor
- 適用範圍:數理科學
簡介,除子,韋伊除子,卡吉耶除子,
簡介
一個卡吉耶除子如果是自然映射 (M*X/𝓞*X)的像,則稱為主除子。如果兩個卡吉耶除子相差一個主除子,則兩個卡吉耶除子稱為是線性等價的。
(M*X/𝓞*X)的像,則稱為主除子。如果兩個卡吉耶除子相差一個主除子,則兩個卡吉耶除子稱為是線性等價的。

除子
[divisor]
在代數幾何中,除子是代數簇的余維數為1的子簇的推廣。有兩種常用的除子:韋伊除子(Weil divisor)和卡吉耶除子(Cartier divisor)。
韋伊除子
韋伊除子就是指代數簇或解析空間X里余維數為1的不可約閉子空間Y的形式的有限整線性組合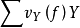 。當所有的
。當所有的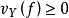 時,韋伊除子構成一個群Div(X)。當X是光滑代數簇時。韋伊除子的概念與余維數為1的代數閉鏈的概念相同。
時,韋伊除子構成一個群Div(X)。當X是光滑代數簇時。韋伊除子的概念與余維數為1的代數閉鏈的概念相同。
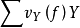
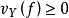
設X是正規概形,f是X上有理(解析的情形為亞純)函式,主韋伊除子(principal Weil divisor)被典範的定義為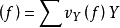 。這裡
。這裡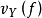 是 f 在𝓞X,Y里的代表元關於子簇Y的環𝓞X,Y的離散賦值,
是 f 在𝓞X,Y里的代表元關於子簇Y的環𝓞X,Y的離散賦值,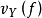 是個整數,且除了有限多個Y之外,
是個整數,且除了有限多個Y之外,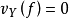 。如果
。如果 ,其中
,其中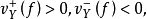 則韋伊除子
則韋伊除子 稱為零點除子(divisor of the zeros),
稱為零點除子(divisor of the zeros),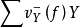 稱為函式f的極點除子(divisor of the poles)。
稱為函式f的極點除子(divisor of the poles)。
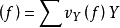
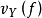
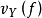
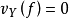

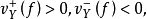

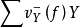
若兩個韋伊除子的差是一個主韋伊除子,則稱這兩個除子線性等價(linear equivalent)。Div(X)關於線性等價的商群稱為概形X的除子類群(divisor class group),記為CI(X)。
卡吉耶除子
卡吉耶除子是指環空間(X,𝓞X)上除子的芽層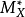 /𝓞*X的一個整體截面。這裡MX表示X上亞純(或有理)函式的芽層,即使得每個開子集
/𝓞*X的一個整體截面。這裡MX表示X上亞純(或有理)函式的芽層,即使得每個開子集 對應環
對應環 (U,𝓞X)的全分式環的層,而
(U,𝓞X)的全分式環的層,而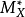 和𝓞*X則分別是
和𝓞*X則分別是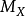 和𝓞X里可逆元的層。一個卡吉耶除子可被一族局部方程
和𝓞X里可逆元的層。一個卡吉耶除子可被一族局部方程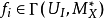 所確定,其中{ Ui } 是X的開覆蓋,函式
所確定,其中{ Ui } 是X的開覆蓋,函式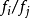 則是層𝓞*X在
則是層𝓞*X在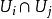 上的截面。一個卡吉耶除子如果是自然映射
上的截面。一個卡吉耶除子如果是自然映射 (M*X/𝓞*X)的像,則稱為主除子。兩個卡吉耶除子稱為是線性等價的,如果二者相差一個主除子。使得
(M*X/𝓞*X)的像,則稱為主除子。兩個卡吉耶除子稱為是線性等價的,如果二者相差一個主除子。使得 𝓞*Xx的x∈M的集合稱為除子的支集(support of the divisor )。卡吉耶除子類
𝓞*Xx的x∈M的集合稱為除子的支集(support of the divisor )。卡吉耶除子類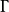 (M*X/𝓞*X)關於線性等價的商群記為CaCI(X)。
(M*X/𝓞*X)關於線性等價的商群記為CaCI(X)。