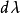主極大

光柵是由大量等寬等間距的平行刻痕所組成的光學器件，稱為衍射光柵。當一束單色平行光照射在N條刻痕的光柵上，每一狹縫都產生衍射。各個狹縫的衍射光經透鏡會聚疊加到處於透鏡焦平面的螢幕上，但是螢幕上每一點的光強分布並不等於1個單縫光強的N倍，而是有的地方條紋又細又亮，相鄰兩個條紋之間是很大範圍的無光黑暗區域。這是因為光經過光柵時，不僅每個狹縫發生衍射，而且縫與縫之間的衍射光波相遇疊加時還要發生干涉。螢幕上呈現的是由每個縫的衍射和縫之間干涉的總效果，稱為光柵衍射條紋，衍射光柵的明條紋特別亮，稱為主極大。

基本介紹

• 中文名：主極大
• 外文名：primary maximum
• 所屬學科：物理
• 相關概念：光柵，光柵衍射，次極大等

光柵衍射的主極大

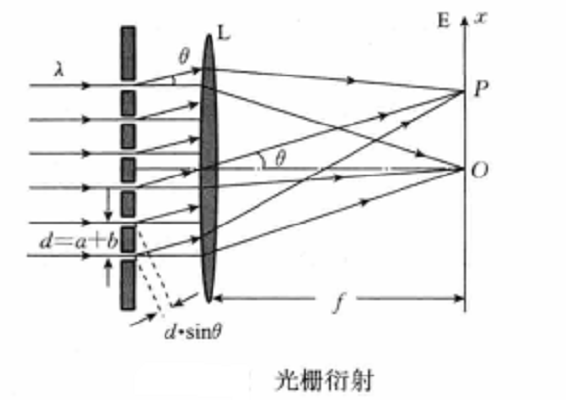
如圖1所示，當一束單色平行光照射在N條刻痕的光柵上，每一狹縫都產生衍射。各個狹縫的衍射光經透鏡會聚疊加到處於透鏡焦平面的螢幕上，但是螢幕上每一點的光強分布並不等於1個單縫光強的N倍，而是有的地方條紋又細又亮，相鄰兩個條紋之間是很大範圍的無光黑暗區域。這是因為光經過光柵時，不僅每個狹縫發生衍射，而且縫與縫之間的衍射光波相遇疊加時還要發生干涉。螢幕上呈現的是由每個縫的衍射和縫之間干涉的總效果，稱為光柵衍射條紋。

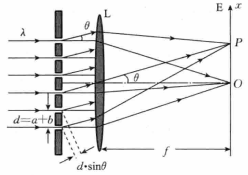圖1光柵衍射

下面討論產生明條紋的衍射方向以及條紋的位置。考察相鄰兩縫的中心點發出衍射角為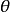的平行光到P點的光程差，由圖1可知，光程差為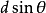。可以證明，如果相鄰兩條縫發出的衍射角為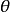方向的衍射光到達P點處的相位為同相時，那么其他縫發出的衍射角為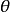方向的衍射光到達P點處的相位也為同相。由此可得，當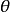滿足以下光柵方程時

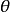
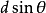
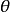
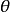
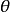
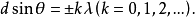
所有縫發出的衍射光到達P點時都是同相的。它們在P點處發生干涉相長形成亮條紋。合振動的振幅是1個縫在該處衍射光振幅的N倍。光強度則為1個縫在該處衍射光強度的N²倍。一般光柵都有幾千條甚至上萬條狹縫，所以衍射光柵的明條紋特別亮，稱為主極大，k的取值就是主極大條紋的級數。衍射角為0時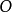，點是中央零級明紋情形。

衍射光柵

一般光源發出的光波都包含多種波長，通常稱為複色光。而許多光學儀器需要單色光源，通常可變波長的單色光源都是從複色光源分光獲得。不僅作為光源很多情況下需要將複色分開，變為單色光。而且因為各種元素都有其特定波長的發射和吸收譜線．通過檢測物質發射或吸收的多種波長的混合光波中是否存在某種特定波長就可以確定其中是否含有某一元素。上述兩種情況都需要一種將不同波長的光分解開的裝置。稜鏡具有分光作用，但分光本領有限，有時不能滿足實際的需要，下面要討論的光柵是另外一種具有很強分光本領的光學器件。

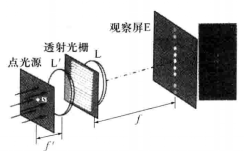圖2點光源的光柵衍射

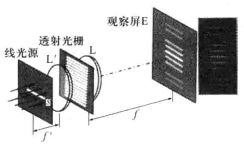圖3線光源的光柵衍射

光柵是由大量等寬等間距的平行刻痕所組成的光學器件，稱為衍射光柵。衍射光柵有兩種：一種是利用透射光衍射的光柵，稱為透射光柵；另一種是利用反射光衍射的光柵，稱為反射光柵。透射光柵常用玻璃製成。玻璃片上刻有大量等寬等間距的平行刻痕，在每條刻痕處，入射光向各個方向散射，而不易透過。兩刻痕之間的光滑部分可以透光，相當於狹縫。透光部分(狹縫)的寬度a和刻痕的寬度b之和d=a+b稱為光柵常量，它是光柵的一個重要參數。

光柵衍射光的極小和次極大

下面利用類似半波帶的方法討論衍射光柵形成極小的條件。如果衍射角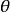滿足

或

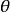
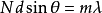
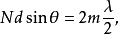
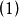
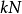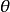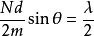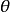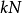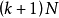式(1)中，m取除之外的整數。各狹縫衍射光的方向滿足上式情況下，N個狹縫被分為2m等份，每2等份為1對，共有m對，與單縫情況中的偶數個半波帶相對應。光柵上相距的子波源發出的衍射角為的平行光的光程差為，所以，每相鄰的時，從一邊數起第1條狹縫與第51條狹縫(第2條狹縫與第52條狹縫，…，第50條狹縫與第100條狹縫)方向的衍射光，在螢幕上匯聚點干涉抵消，形成1級極小。由於從到之間m共有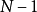個取值，所以從第k級到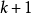級主極大之間有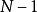個極小。兩個極小之間還應有一個次極大。在實際情況下，由於N值特別大，次極大被淹沒在雜散的背景光之中，觀察不到，所以兩個相鄰的主極大之間是大範圍的黑暗區域，光柵衍射的光強都集中在主極大的範圍內，所以條紋特別窄、特別亮，其光強分布如圖4所示。

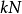
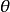
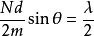
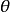
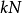
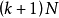
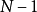
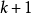
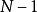
圖4 光柵衍射的強度分布及缺級

缺級

如果某些衍射方向即滿足光柵方程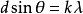，同時又滿足單縫衍射極小條件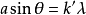，則k級主極大不出現，這種情況稱為缺級，如圖4的第3級為缺級。這是因為每個單縫θ方向的衍射光疊加均為0，N個單縫的光疊加等於N個0相加仍然為0；如果第k級缺級，則2k，3k，…均不出現。光柵條紋中出現缺級的條件是。

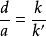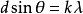
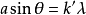
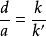
主極大條紋寬度和光柵的分辨本領

光柵衍射主極大的角(線)寬度定義為距離明紋中心最近的兩個極小之間的角(線)距離。即第k級主極大的角寬度等於第kN+1級極小與第kN-1級極小的衍射角之差。將光柵衍射極小條件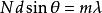具體化為第kN+1級極小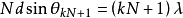和第kN-1級極小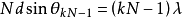相減，可得到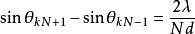。又由於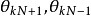相差很小，利用高等數學函式增量很小時近似等於它的微分的關係可得，其中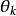為k級主極大的衍射角。所以第k級主極大的角寬度和線寬度分別為

為透鏡焦距。以上兩式表明光柵縫數越多，N值越大，主極大明條紋越窄；條紋級數越高，k值越大，就越小，條紋越寬。由於每個單縫在各衍射方向上的光強度不同。所以在該方向上N個縫疊加產生的主極大亮度也不同。光柵衍射主極大的振幅的包羅線就是N個單縫振幅曲線的算術疊加。

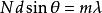
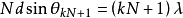
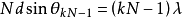
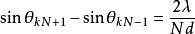
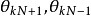
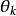
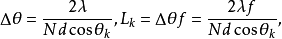
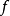
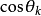
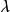前面我們研究了單色平行光經光柵後產生主極大明條紋的條件及主極大條紋的寬度。如果入射的是複色平行光，經光柵衍射後，除了0級主極大各種波長的光仍然重合之外，其他級數的主極大中，不同波長的明條紋在屏上位置不同，而且，級數越高分開得越遠。這樣，光柵就起到分光的作用。那么，對於一個光柵來說，波長相差多少的光波能被分開呢?影響光柵分光本領的因素有哪些?我們將光柵方程兩邊微分可得，此式說明波長和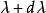的兩個波長第k級主極大的衍射角相差

由瑞利判據可知，當兩個波長的k級明條紋中心的距離大於等於該級主極大明條紋寬度的一半時，也就是當滿足條件時，這兩個波長的k級主極大條紋能夠分辨開。把和代入到中就能得到

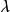
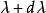
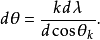
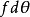
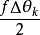
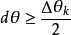
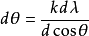
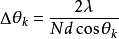
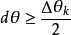
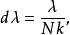
此式說明用一塊具有N條狹縫的光柵分光，在第k級所能分開的兩個波長之差正比於光波的波長，反比於光柵縫數與級數之積，與光柵常量無關。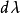值越小，光柵的分光本領越高，所以用於分光的光柵縫數達上萬條。