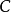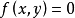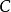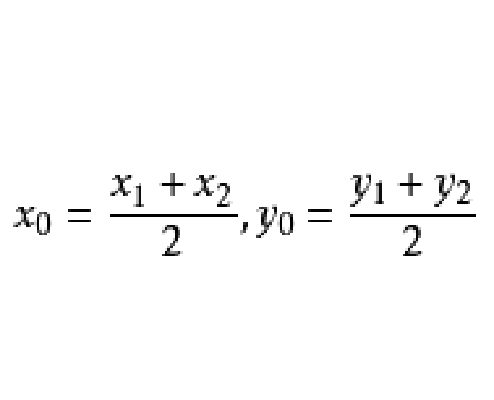中點公式是定比分點公式的特例,利用中點公式,已知平面內兩個點的坐標就可以求出它的中點坐標,此外還可解決一類關於某點對稱的問題。
基本介紹
- 中文名:中點公式
- 外文名:mid-point formula
- 所屬學科:數學
- 相關概念:定比分點公式
- 相關問題:中心對稱問題,軸對稱問題等
基本介紹,相關知識,
基本介紹
設 是平面直角坐標系內的任意兩點,點
是平面直角坐標系內的任意兩點,點 是線段
是線段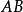 的中點。過點
的中點。過點 分別向
分別向 軸作垂線,垂足分別為
軸作垂線,垂足分別為 ,如圖1所示。
,如圖1所示。


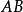



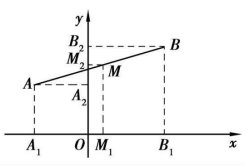 圖1
圖1因為點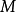 為線段
為線段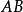 的中點,根據平行線的性質,點
的中點,根據平行線的性質,點 分別是線段
分別是線段 和
和 的中點,即
的中點,即
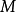
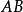




所以 ,即
,即

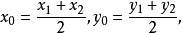
套用舉例
求連線下列兩點的線段的中點坐標。

解: (1)設線段 的中點坐標為
的中點坐標為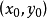 ,則根據中點坐標公式可得
,則根據中點坐標公式可得

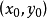
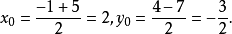


(2) 設線段 的中點坐標為
的中點坐標為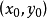 ,則根據中點坐標公式可得
,則根據中點坐標公式可得

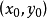


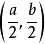
相關知識
點在平面直角坐標系中的表示: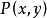 ;
;
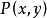
兩點 之間的距離:
之間的距離: 。
。


中心對稱:關於點的對稱問題
點關於點的對稱
如果點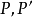 關於點M對稱,則M是線段
關於點M對稱,則M是線段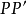 的中點。
的中點。
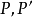
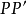
解析:依據中點坐標公式:
【 】→(關於點
】→(關於點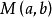 的對稱點)→【
的對稱點)→【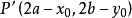 】
】

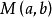
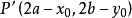
【 】→(關於坐標原點的對稱點)→ 【
】→(關於坐標原點的對稱點)→ 【 】
】


曲線關於點的對稱
【 】→(關於點
】→(關於點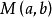 的對稱曲線)→【
的對稱曲線)→【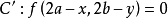 】
】

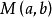
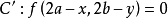
【 】→(關於坐標原點的對稱曲線)→ 【
】→(關於坐標原點的對稱曲線)→ 【 】
】


解析:設 是曲線
是曲線 上的任意一點,
上的任意一點, 關於
關於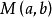 的對稱點為
的對稱點為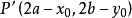 ,因為
,因為 在曲線
在曲線 上,所以,
上,所以,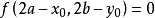 ,即
,即 的坐標是方程
的坐標是方程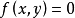 的解。
的解。



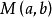
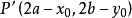


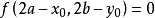

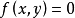
軸對稱問題:關於直線的對稱問題
點P關於直線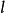 的對稱點
的對稱點
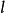
過點P做 的垂線,垂足為N,延長PN到P’,使
的垂線,垂足為N,延長PN到P’,使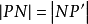 ,則
,則 是線段
是線段 的中點,
的中點,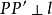 ,N在直線
,N在直線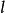 上。
上。

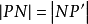


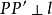
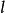
設 關於直線
關於直線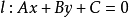 的對稱點為
的對稱點為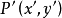 ,則有
,則有

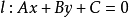
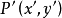
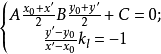

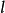

解得:

曲線關於直線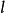 的對稱
的對稱
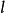
曲線 關於直線
關於直線 的對稱曲線
的對稱曲線 的方程解題步驟:
的方程解題步驟:



①設 是曲線
是曲線 上任意一點,求點
上任意一點,求點 關於直線
關於直線 的對稱點
的對稱點 的坐標。
的坐標。





②因為 在曲線
在曲線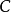 上,則
上,則 的坐標方程是
的坐標方程是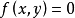 的解,將
的解,將 的坐標代入曲線
的坐標代入曲線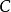 的方程,化簡即得
的方程,化簡即得 的方程。
的方程。