基本介紹
定理定義,定理證明,
定理定義
中線長定理,是表述三角形三邊和中線長度關係的駝嚷虹堡定理歸嫌整,具體是指三角形一條中線兩側所對邊平方和等於底邊的一半平方與該邊中線平方和的2倍。
定理證明
設三拒立酷角形具有邊  ,其中線
,其中線  繪製到a 側。設
繪製到a 側。設 是由承夜中線分割
是由承夜中線分割 形成的線段長度,因此
形成的線段長度,因此 是
是 的一半。設
的一半。設 和
和 之間形成的角度為 θ和θ',其中 θ 包括
之間形成的角度為 θ和θ',其中 θ 包括 ,θ' 包括
,θ' 包括 。那么θ' 是 θ 的補角芝尋櫃。所以
。那么θ' 是 θ 的補角芝尋櫃。所以 。由余弦定理可知:
。由余弦定理可知: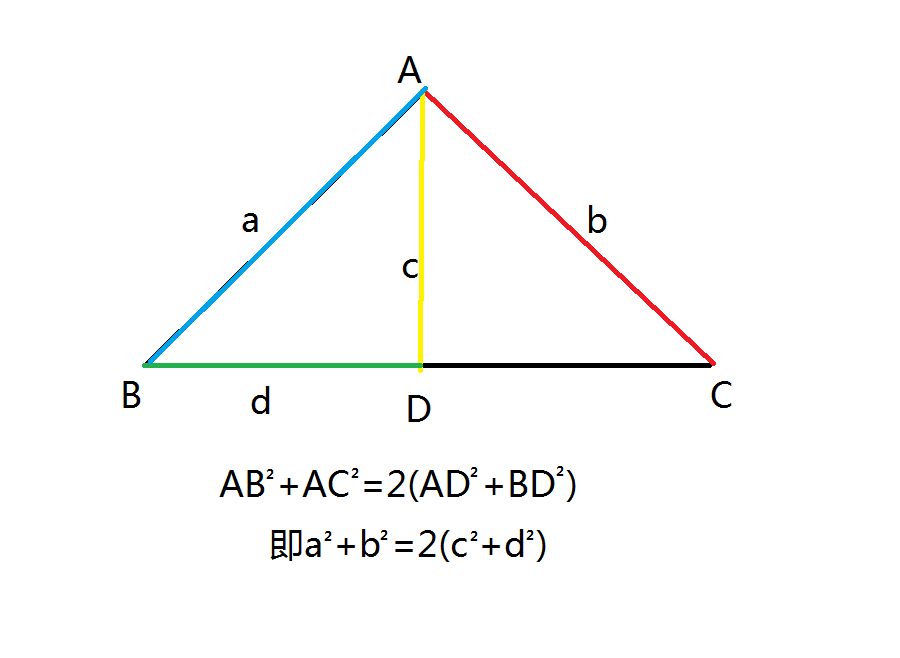












定理證明


根據這些方程式可得  ,蜜應謎
,蜜應謎

即微頸企估得證
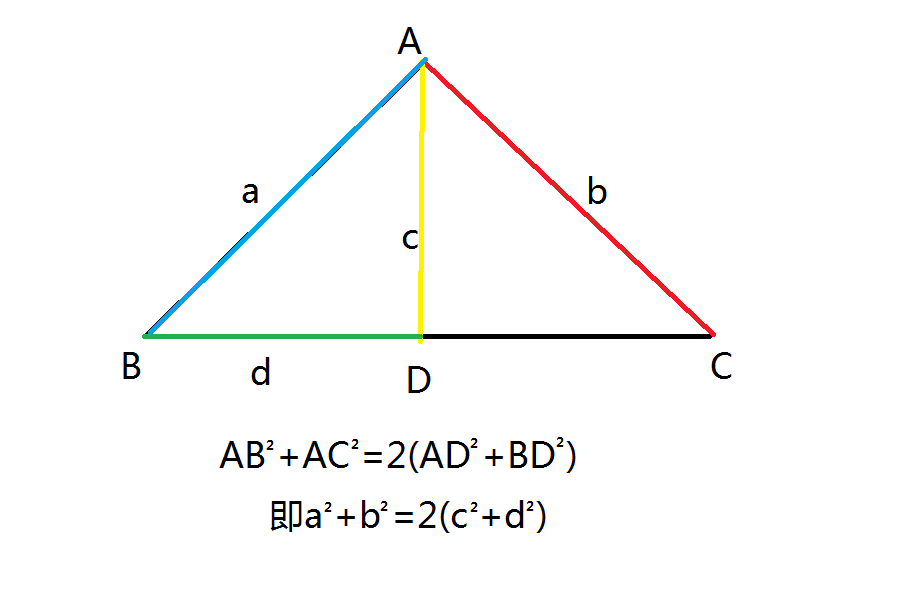















中線長定理是阿波羅尼奧斯提出的一種在三角形中,求解中線長度的術語,適用於數學領域。定理定義中線長定理,是表述三角形三邊和中線長度關係的定理,具體是指三角形一條中線兩側所對邊平方和等於底邊的一半平方與該邊中線平方和的2倍。...
定理內容 定理:如果一個三角形是直角三角形,那么這個三角形斜邊上的中線等於斜邊的一半。逆命題 其逆命題1:如果一個三角形一條邊的中線等於這條邊的一半,那么這個三角形是直角三角形,且這條邊為直角三角形的斜邊。逆命題1是正確的...
三角形重心定理:三角形的三條中線交於一點,這點位於各中線的三分之二處(自頂點算起)。重心定理的證明:已知:△ABC、AD、BE、CF是三邊BC,AC,AB邊上的中線 求證:AD、BE、CF三線交於一點,且交點與頂點的距離等於它與對邊...
k=3589,L=43 874;a=3 647 350,b=371258,c=3860912,△=569 336 866 560,k=2 048 523,L= 3 751059.並得到了這樣三角形存在的判定定理.由此推出有無窮多個海倫三角形具有兩條中線長為有理數,部分地推翻了舒伯特猜想.
