基本介紹
- 中文名：中程數
- 外文名：Mid-range
- 學科：數學
- 基本釋義：數據中的最大值和最小值的均值
- 是：反映數據集中趨勢的一項指標
- 領域：統計學
定義,性質分析,魯棒性,效率,採樣性質,其它統計數據,
定義
在統計學中，中程數是一組統計數據值的最大值和最小值的算術平均值
。中程數是反映數據集中趨勢的一項指標。
計算示例：
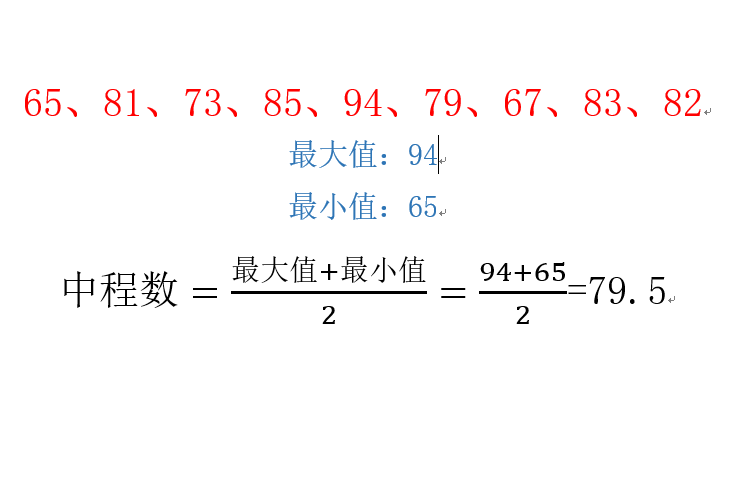
求下列數的中程數：65、81、73、85、94、79、67、83、82
解：最大值=94，最小值=65，則中程數=
性質分析
魯棒性
中程數，對極大值和極小值是異常高度敏感，並且會忽略除極大值和極小值之外的所有數據點，所以它是一個非常不可靠的統計數據。此外，增加樣品的最大值或者減少樣品的最小值都會改變中程數的值。因此，在實際的統計數據中沒有什麼用處，除非已經處理異常值。
效率
中程數可以高效地估計出給定足夠低峰態分布的小樣本的
，但它對於常態峰分布是低效的，如常態分配。對於一個未知最大值和最小值的連續均勻分布，中程數是平均值的最小方差無偏估計。
採樣性質
對於一個大小為n的標準常態分配，中程數M是無偏的，其方差為：
對於一個大小為n的標準拉普拉斯分布，中程數M是無偏的，其方差為：
特別地，當樣本大小n增加時，方差不會降至零。
其它統計數據
均值/平均數/算數平均數
平均數是表示一組數據集中趨勢的量數，是指在一組數據中所有數據之和再除以這組數據的個數。它是反映數據集中趨勢的一項指標。
如數據23，29，20，32，23，21，33，25的均值為：= （23+29+20+32+23+21+33+25）÷ 8 = 25.75
中位數
中位數是按順序排列的一組數據中居於中間位置的數。一般首先將數據從小到大（或從大到小）排序，尋找“中間”的數值（當數據集中有偶數個數值時，中位數取中間兩位數的均值） 。它也是反映數據集中趨勢的一項指標。
如數據20，21，23，23，25，29，32，33 的中位數為：（23+25）÷2 = 24
眾數
眾數是數據集中出現頻率最多的數字，它不唯一。
如數據20，21，23，23，25，29，32，33 的眾數是23
極差
如數據20，21，23，23，25，29，32，33 的中位數極差：33 - 20 = 13
