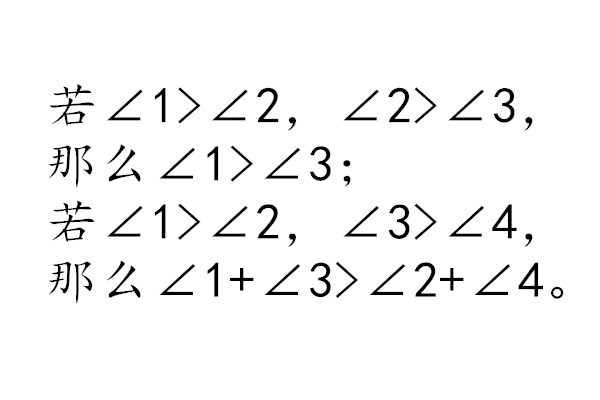基本介紹
- 中文名:不等量公理
- 外文名:axioms of inequality
- 所屬學科:數學
- 簡介:解不等式的依據
- 屬性:數學的基本公理之一
基本介紹,例題解析,
基本介紹
不等量公理常指以下公理:
(1)不等量加上或者減去等量,原來大的仍大;
(2)不等量乘以或者除以同一個正數,原來大的仍大;
(3)不等量加不等量,大量的和大於小量的和;
(4)等量減不等量,減去大的,差反而小;
(5)第一量大於第二量,第二量大於第三量,則第一量大於第三量;
(6)全量大於它的任何一部分;
(7)在不等式中,一個量可以用它的等量來代替。
在研究不等關係時,常要用到一些關於不等量的公理。其中有些我們在學習代數時已經在套用,如:不等量加上或者減去等量,原來大的仍舊大;不等量乘以或者除以同一個正數,原來大的仍舊大;在不等式中,一個量可以用它的等量來代替。此外,還常用到下面一些不等量的公理:
(1)第一量大於第二量,第二量大於第三量,第一量就大於第三量。例如,∠1>∠2,∠2>∠3,那么∠1>∠3。
(2)不等量加不等量,大量的和大於小量的和。例如∠1>∠2,∠3>∠4,那么∠1+∠3>∠2+∠4。
(3)全量大於它的任一部分量。例如,C是線段AB上一點,那么AB>AC。
例題解析
【例1】 證明:從直線外一點到這條直線上各點所聯的線段中,和這條直線垂直的線段最短。
已知:PO⊥AB,O為垂足,E為AB上異於O的一點,
求證: PE> PO。
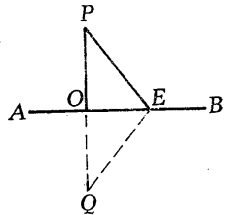 圖1
圖1證明:延長PO至Q,使PO= OQ,
以AB為軸翻轉P點所在的半平面(圖1)。
∵PO⊥AB,(已知),
∴翻轉後射線OP與OQ重合,
又OP= OQ,
∴P、Q重合,
則 PE= EQ,
PE+EQ= 2PE,
但PQ<PE+EQ,(兩點間所連線段最短)
∴PO<PE (不等量公理)。
【例2】D為△ABC內一點(圖2),求證∠BDC>∠A。
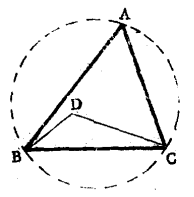 圖2
圖2此題除可利用有關定理來證,還可以利用不等量公理。
分析1 根據“等量減不等量,減去大量的差反而小”,設法找一個等式,使它的兩端分別含有∠BDC和∠A,然後從等量減去不等量,剩餘的就是∠BDC與∠A的關係。
在△DBC和△ABC中,由三角形的內角和定理可得等式:
∠BDC+∠DBC+∠DCB=∠A+∠B+∠C,
又∠DBC+∠DCB<∠B+∠C,
∴∠BDC>∠A。
分析2 根據“不等量加不等量,大量的和大於小量的和”,可將∠BDC和∠A都分成兩個角的和,再由每一部分 的大小關係得出整個角的大小關係。最簡單的分法是連結AD並延長使之交BC邊於E(圖3),由外角定理不難得到∠BDE>∠BAE,∠EDC>∠EAC,相加得∠BDC>∠BAC。
 圖3
圖3