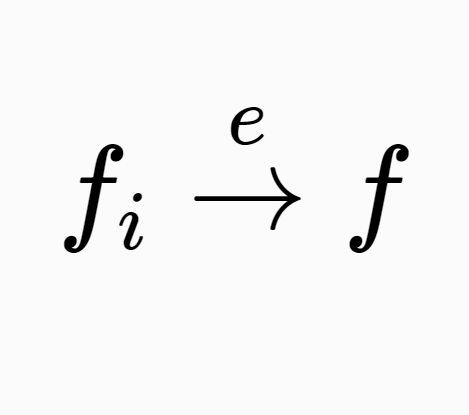上圖收斂性

上圖收斂性(epigraph convergence)是最最佳化逼近理論中的收斂性質。大部分非線性規劃算法只有在目標函式和約束條件函式表達式明顯給出，且其逐次疊代過程中在各疊代點處的函式值與梯度向量的計算不很困難時可以使用，否則，使用這些方法的可行性就成問題，或者使用這些方法的代價太大。這時，往往用逼近方法求解所給規劃問題，即用較簡單的函式來逼近目標函式或約束條件函式，用逼近函式形成的規劃問題的解作為原問題的解的近似，在最最佳化逼近理論中，有許多種函式序列的收斂性，上圖收斂性(Epigraph Convergence)是其中最有力的一種。

基本介紹

• 中文名：上圖收斂性
• 外文名：epigraph convergence
• 所屬學科：數學（非線性規劃）
• 所屬問題：最優逼近理論
• 簡介：最最佳化逼近理論中的收斂性質

基本介紹

上圖收斂性是最最佳化逼近理論中的收斂性質， 上函式f的上圖是指 中的集合：

若給定 ，則可完全確定這個函式，即

因此，集合 的性質與函式f的性質有著決定性的聯繫：f為下半連續函式若且唯若 為 中的閉集；f為凸函式若且唯若 為凸集，根據函式與它的上圖之間的一一對應關係，可用上圖序列的收斂性來研究函式序列的收斂性，而上圖序列的收斂性即是集合序列的收斂性。

有如下相關的理論：如果

稱集合序列收斂於S，這時記為

或

其中 { |存在 使得 ，且除了有限多個i外都有 }， {|存在子序列 使得 ，且 }，對於 與 ，下面的關係式成立：

式中clA表示集合A的閉包，對任何集合序列，有

式中H為自然數集的子集，K為N的下列形式的子集的全體：(n為某一自然數)，N為N的所有無限子集的全體，對任一序列，和均為閉集。對任何集合序列，包含關係成立。

若有，則稱函式序列上圖收斂於f，記為，這時，

並稱f為的epi極限。如果

1.對任一x和任一收斂於x的序列，有

2.對任一x，總存在收斂於x的序列，使得

則函式序列上圖收斂於f。

相關性質及討論

無約束最最佳化問題的逼近理論是：設有一系列極小化問題，其中為一族下半連續函式，且，則

其中，若為非空集合，Z為有限數，則;若進一步有收斂序列，則，設，且存在一個緊緻集合D，使得對每一i，非空，則必有。

約束最最佳化問題的逼近理論是：設，則它等價於無約束最最佳化問題

式中

此問題的近似問題為

式中集合序列在某種意義下收斂於S;；或

式中函式序列在某種意義下收斂於f，設問題(1)與(2)中的f為連續函式，

則，式中，

設，S為豐滿閉集(即)，f為連續函式，則，式中

上圖收斂性是指：若f是函式序列的epi極限，則f一定是下半連續函式。設，且所有f_i為凸函式，則f亦為凸函式.

凸函式f在點處的次梯度的集合稱為次微分，定義為，故次微分函式為集值函式，它的圖形G(∂f)定義為

有下面的結果：設為凸函式序列，則若且唯若

設對任一x，序列單調收斂於f(x)，式中f為下半連續函式，則上圖收斂於f；反之，若為單調序列，，則亦依點收斂於f。