三階積幻方

什麼是三階積幻方？如下圖就是一個三階積幻方。

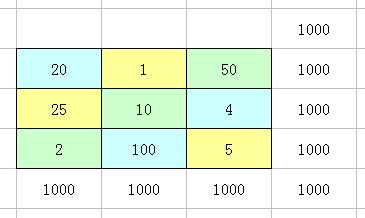
三階積幻方的填法

什麼樣的自然數能構成3階積幻方呢？

我先說3階和幻方。1-9的數每3個數分成一組，如【1、2、3】、【4、5、6】、【7、8、9】，下圖是用1-9構成的3階和幻方，幻和值=15 。

再說3階積幻方。

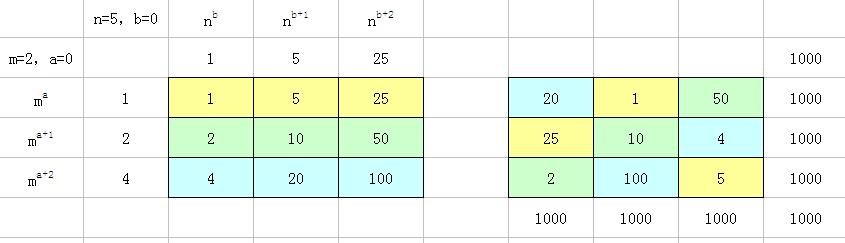
如下圖左圖，行為n的不同次冪，列為m的不同次冪，中間九個格中為不同行列基數的乘積。

下圖右圖，是用9個格中的數，依據3階和幻方的構成方式組成的3階積幻方。

舉例：

例1：取n=3，b=0；m=2，a=0。

下圖左圖得到3個一組9個數：【1、3、9】、【2、6、18】、【4、12、36】

下圖右圖為這9個數構成的3階積幻方，幻積值=6^3=216。

例2：取n=5，b=0；m=2，a=0。

下圖左圖得到3個一組9個數：【1、5、25】、【2、10、50】、【4、20、100】

下圖右圖為這9個數構成的3階積幻方，幻積值=10^3=1000。

簡單地說：【3個數一組的3組數（共9個數），組與組倍數相等，每組數與數倍數相等】，這樣的數能構成3階積幻方。

將這3組九個數，按三階和幻方相同的填寫方式填入幻方，這樣完成的幻方每行、每列和兩條對角線的3個數的乘積相等。

三階積幻方的幻積值=中間數的3次方。