三角形的一條邊與另一條邊的延長線組成的角,叫做三角形的外角。三角形外角和是360°(多邊形的外角和一般是每個頂點只取一個外角計算而得)。
基本介紹
- 中文名:三角形的外角
- 外文名:Triangle outside
- 第一條:正文
- 第二條:定義
- 第三條:性質
定義,性質,
定義
三角形有6個外角。外角的個數等於多邊形邊數的兩倍。
三角形外角和是360°(多邊形的外角和一般是每個頂點只取一個外角計算而得)
性質
三角形的一個外角等於與它不相鄰的兩個內角的和。.
三角形的一個外角大於與它不相鄰的任一內角.
定理:三角形的一個外角等於不相鄰的兩個內角和。
定理:三角形的三個內角和為180度。(三角形內角和定理) 定理:多邊形的外角和都等於360度。 拓展:在三角形中,已知其中兩個角的度數,根據三角形內角和定理,則能求出第三個角的度數。
三角形的外角平分線定理:三角形的外角平分線外分對邊所成的兩條線段和相鄰兩邊對應成比例。
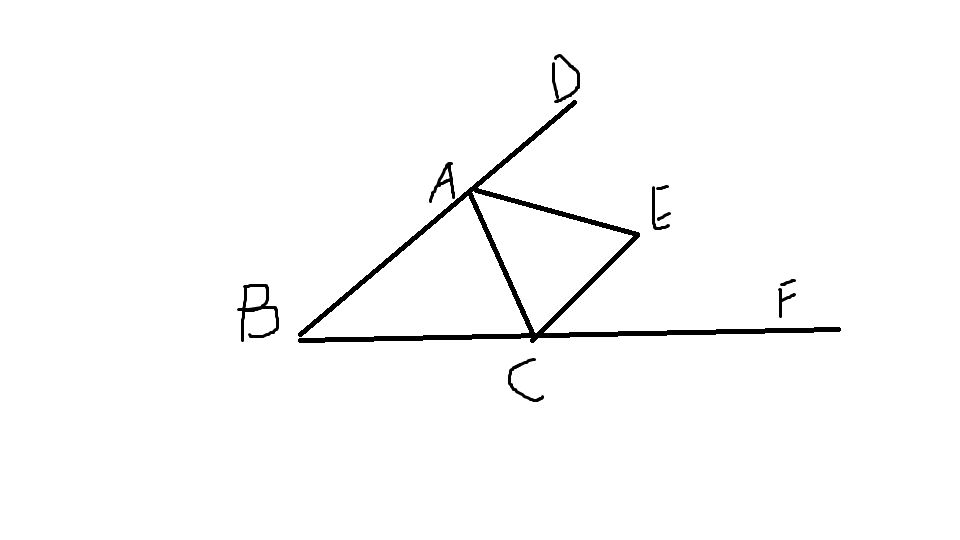
例.已知如圖.△ABC中,∠BAC的外角平分線交BC的延長線於點 D,求證:BD︰CD=AB︰AC。
證明:過C作AD的平行線交AB於點E。
∴BD︰CD=AB︰AE,∠1=∠AEC
∠CAD=∠ACE
∵∠1=∠CAD ∴∠AEC=∠ACE
∴AE=AC ∴BD︰CD=AB︰AC
證明2:
ACD面積=0.5xCAxADxsin(Li)=0.5xCDxh (h為BD邊上的高)
a b
ABD面積=0.5xBDxh=0.5xBAxADxsin(180度-L1)
c d
axc=ACD面積xABD面積=bxd (左右兩邊均約去h,sin,0.5x0.5,AD)
得 CAxBD=CDxBA 變形得 BD︰CD=AB︰AC