三角形線性元素是三角學的基本概念之一指與三角形有關的線段,如三角形的周長、高、中線、角平分線、外接圓半徑、內切圓半徑及旁切圓半徑等。
基本介紹
- 中文名:三角形線性元素
- 外文名:linear elements of a triangle
- 適用範圍:數理科學
簡介,計算公式,周長,高線長,中線長,內角平分線長,外角平分線長,內切圓半徑,外接圓半徑,旁切圓半徑,套用,
簡介
三角形線性元素是三角學的基本概念之一,指與三角形有關的線段,如三角形的周長、高、中線、角平分線、外接圓半徑、內切圓半徑及旁切圓半徑等。
在用有限元素法求解二維問題(包括平面問題及軸對稱問題)時,最簡便可行的方法是:將求解區域進行三角形有限元素分割,取三角形元素的頂點為節點,在每個三角形元素上利用三個頂點上的函式值進行線性插值,並在此基礎上將所考察的泛函離散化,最後引出有限元素法的計算格式而求解。象這樣的元素,稱為三角形線性元素。
計算公式
周長
若三角形的周長用l表示,則
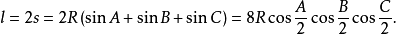
高線長
若三角形的三邊a,b,c邊上的高線長分別用ha,hb,hc表示,則:
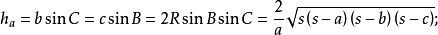
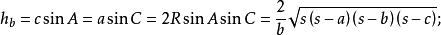
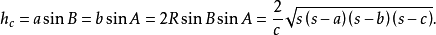
中線長
若三角形的三邊a,b,c邊上的高線長分別用ma,mb,mc表示,則:
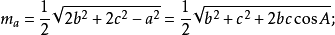
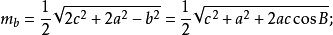
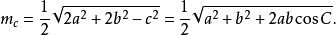
內角平分線長
若三角形的三內角A,B,C的角平分線長分別用ta,tb,tc表示,則:
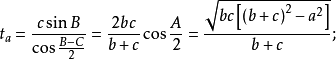
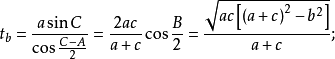
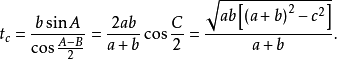
外角平分線長
三角形外角平分線是指內角對邊的延長線和該內角鄰接的外角平分線的交點到該內角頂點線段的長。當無交點時外角平分線長不存在。若三角形的三內角A,B,C的角平分線長分別用ta’,tb’,tc’表示,則:
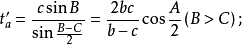
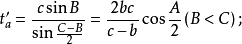
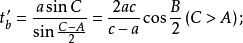
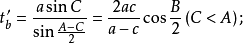
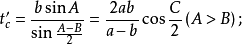
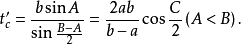
內切圓半徑
若三角形的內切圓半徑用r表示,則
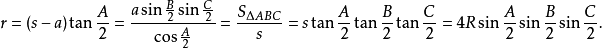
外接圓半徑
若三角形的外接圓半徑用R表示,則
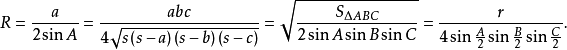
旁切圓半徑
若三角形的三邊a,b,c邊上的旁切圓半徑分別用ra,rb,rc表示,則:
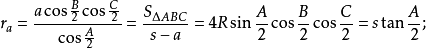
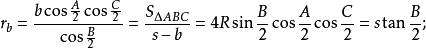
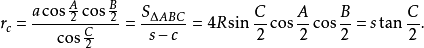
套用
在計算實踐中可以發現,採用三角形線性元素是比較方便的,且能比較靈活地適應不規則的幾何形狀,因而仍不失為是一種簡便有效的方法。但是,由於採用的是線性插值,精度往往不夠理想,例如,在應力分析問題中,它在每個元素中的應力和應變都是常數,因而,特別在應力集中的部位,產生的誤差較大;有時即使在應力集中的範圍內配置極為密集的元素,仍然不能較好地反映應力集中的趨勢,不能給出應力集中因子的比較正確的數值。
