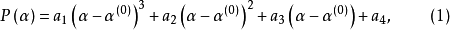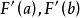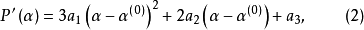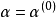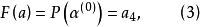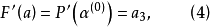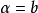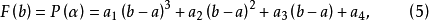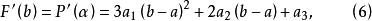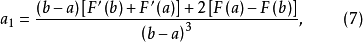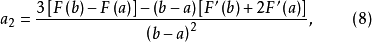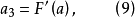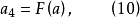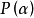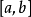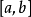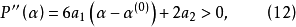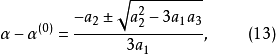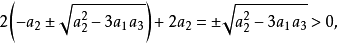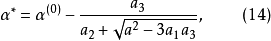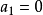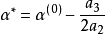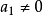三次插值法(cubic interpolation method)是一種多項式插值法,逐次以三次曲線φ(t)=a0+a1t+a2t2+a3t3的極小點逼近尋求函式f(t)的極小點的一種方法.具體做法是:設t1<t2,在搜尋區間[t1,t2]中以φ(t)擬合f(t),使滿足φ(ti)=f(ti),φ'(ti)=f'(ti), (i=1,2)(此式記為(1)式)對φ(t)求導並令其等於零,求得φ(t)在[t1,t2]中由a0,a1,a2和a3表示的極小點表達式,再由方程組(1)解得a0,a1,a2和a3,將其代入此表達式,便得f(t)的近似極小點,逐次疊代,當φ(t)在近似極小點處的導數值的絕對值小於某給定誤差時,疊代停止.用三次插值法尋求極小點一般比用二次插值法(參見“拋物線插值法”)有更快的收斂速度,但其每一輪疊代的計算量則比二次插值法要大。
基本介紹
- 中文名:三次插值法
- 外文名:cubic interpolation method
- 所屬學科:數學
- 簡介:一種多項式插值法
- 提出者:Davidon
基本介紹
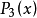
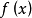
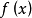
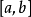

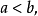
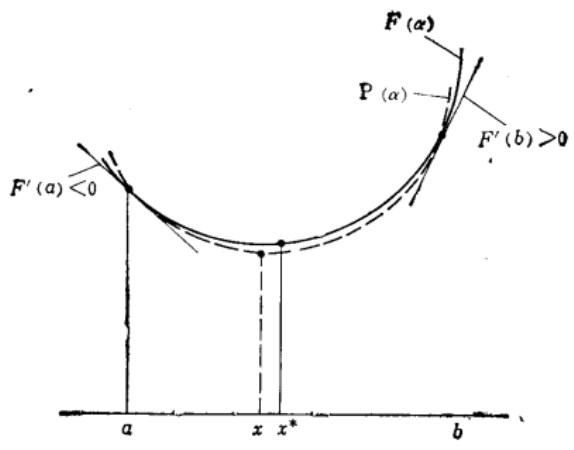
 圖1
圖1相關分析