基本介紹
- 中文名:牛頓三叉曲線
- 外文名:Trident of Newton
- 學科:數學
介紹
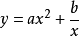
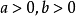
性質
漸近線

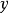
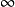
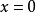

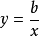

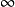
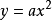
單調性
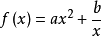
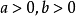
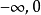
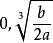
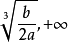
最小值
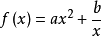
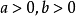

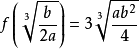
初等證明
單調性
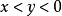
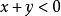
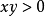
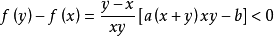
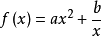
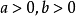
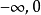
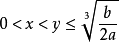
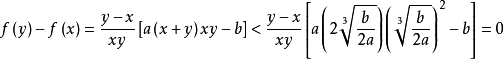
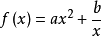
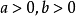
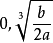
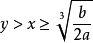
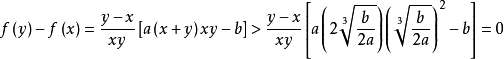
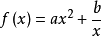
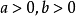
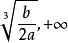
最小值
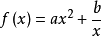
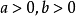

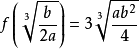
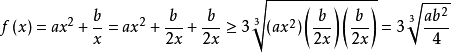
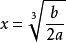

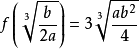
其它各種符號
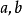
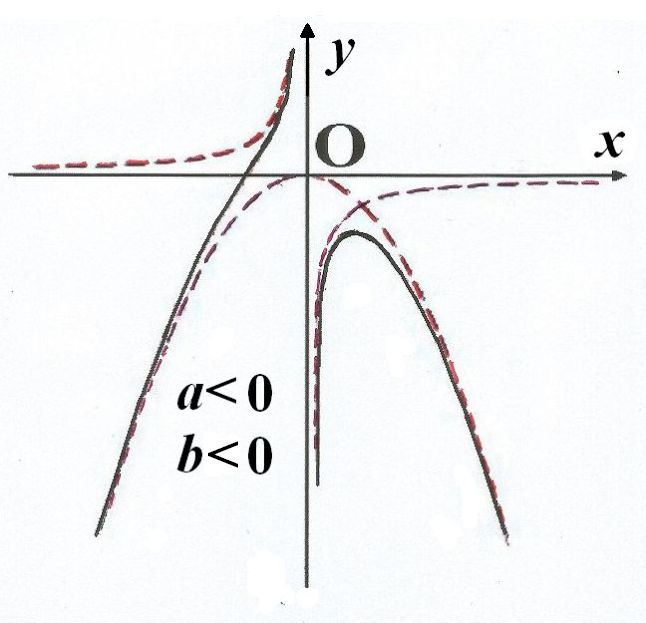
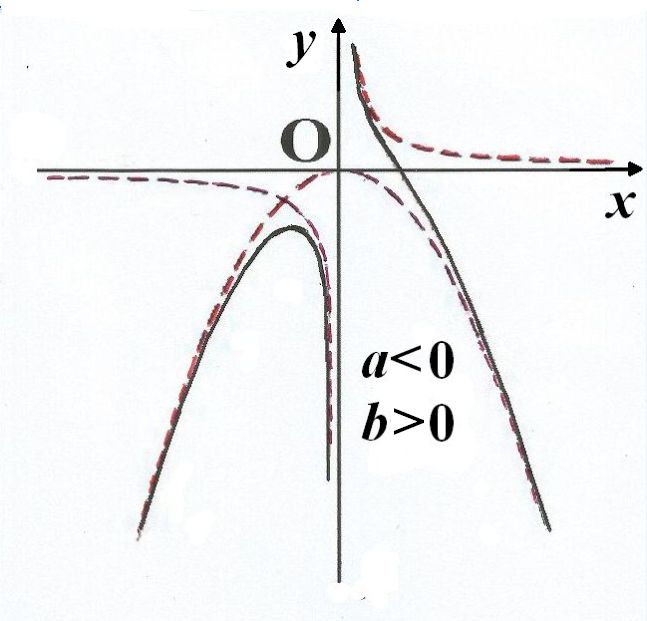
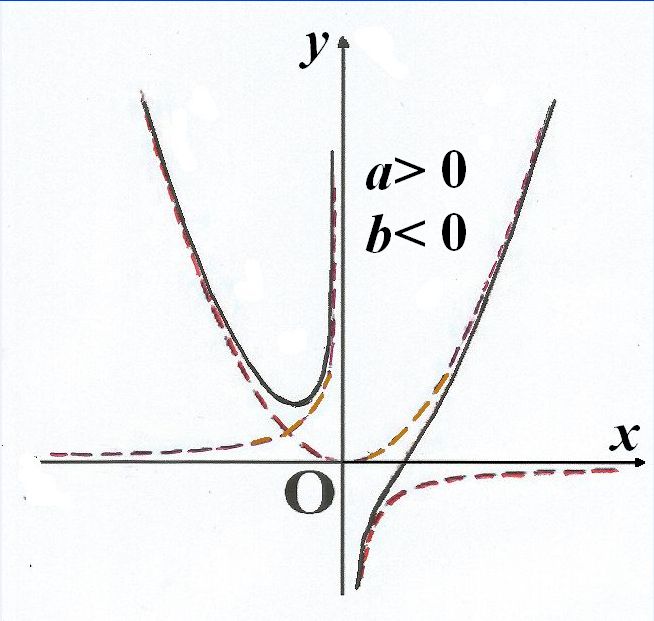
舉例
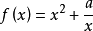
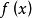
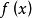
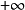

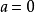
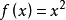
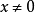
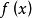
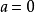
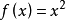
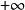
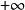
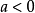
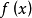
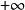
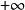
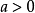
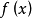
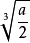
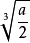
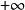
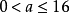


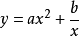
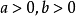

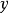
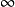
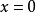

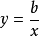

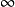
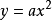
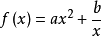
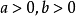
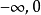
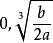
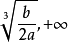
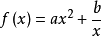
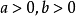

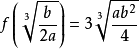
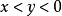
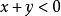
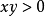
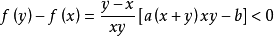
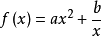
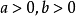
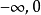
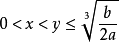
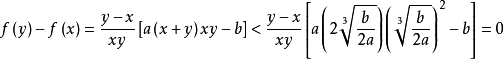
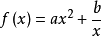
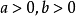
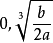
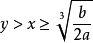
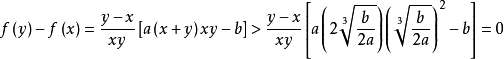
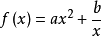
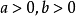
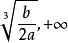
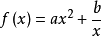
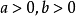

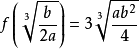
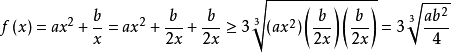
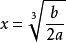

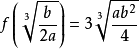
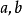



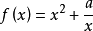
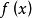
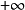

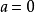
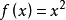
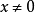
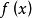
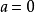
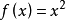
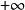
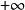
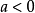
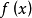
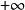
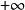
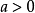
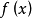
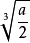
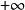
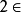
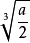
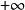
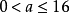


三叉戟是一種多見於神話的雙手用長柄兵器。本為希臘神話中海神——波塞冬的武器。它的外形和長柄的魚叉相似,中間刺較長而兩側的較短。有些時候兩側的尖刺向外彎,...
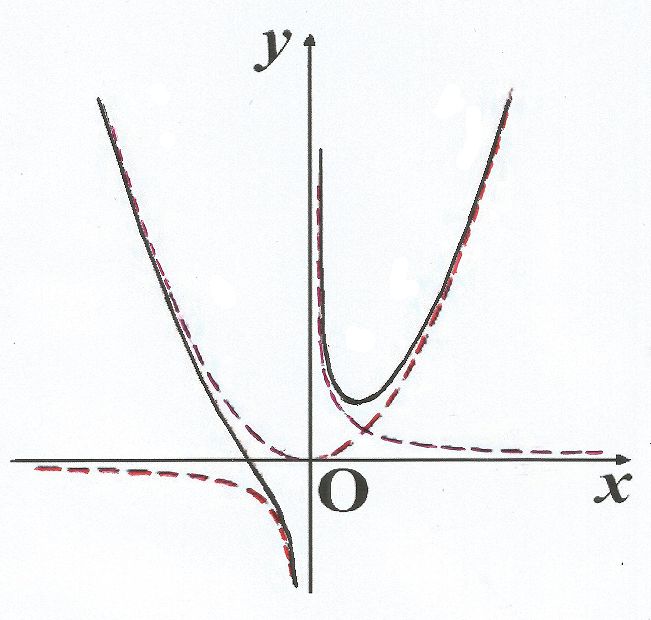
函式y=ax²+b/x(a>0,b>0)的圖像稱為三叉戟曲線。三叉戟是希臘神話中海神波塞冬的武器,而函式y=ax²+b/x的圖像恰如其形,因而得名。牛頓最早研究了...
除此之外,三叉戟這個詞目還廣泛套用於體育比賽中。往往把前場的三名隊員構成的進攻核心稱之為三叉戟。三叉戟在足球比賽中,還可形容為三個前鋒。例如;三叉戟是一...
三叉戟,是瑪莎拉蒂(Maserati)的標誌。瑪莎拉蒂是一家義大利豪華汽車製造商,1914年12月1日成立於博洛尼亞(Bologna),公司總部現設於摩德納(Modena)。1993年菲亞特(Fiat ...
“三叉戟”客機是英國德·哈維蘭公司研製的中短程三發噴氣式民航客機。最初德·哈維蘭公司將其命名為D.H121,後改為“三叉戟(Trident)”。給飛機取名“三叉戟”,...
“如果你不想永遠地扔掉它,你應該給它忠誠魔咒。這個普通的魔咒可以讓你的三叉戟回到你身邊。激流可以讓你在擲出三叉戟時衝刺(在水中或下雨時)那東西也值得你去...
三叉戟是美國三叉戟式潛射洲際飛彈,服役中,分為三叉戟二型、三叉戟一型。美國計畫將它裝在俄亥俄級潛艇上,而後在1989年加入太平洋艦隊,在1992年加入大西洋艦隊。...
劇情簡介二十年前叱吒風雲的三個警察“老炮”,被警界榮稱為“三叉戟”,如今已到了快退休的年紀,卻不料誤打誤撞辦了一起洗錢大案,凍結了巨額贓款。金融巨騙為了...
尼普頓三叉戟(Trident of Neptune)是海王的專屬武器。...... 圖集 尼普頓三叉戟圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1次歷史版本 最近更新: 創建...
羅斯福、英國首相邱吉爾率美英聯合參謀長委員會(由美國參謀長聯席會議和英國參謀長委員會組成)成員在美國華盛頓舉行的會議(代號為“三叉戟”,故亦稱“三叉戟會議”)...
“三叉戟”客機(英文:Trident),是英國霍克.西德利(Hawker Siddeley )公司(後併入英國宇航公司)研製的一款中短程三發噴氣式民航客機。中國在1970年代引進“三叉戟”...
電影《三叉戟》是一部由呂錚編劇的電影作品,影片主要講述了被稱為“三叉戟”的三個警察“老炮”,運用傳統的警察手段進行破案,在對手巨大的利誘下,三人之間的關係...
三叉戟是電視劇《女媧傳說之靈珠》中的兵器。中文名 三叉戟 外文名 trident 登場作品 女媧傳說之靈珠 使用者 問天龍族二殿下問天的兵器,也是龍族的聖物只有...
三叉戟飛彈,美國研製的由潛艇發射的多彈頭飛彈。主要有三叉戟-1、三叉戟-2等多種型號:三叉戟-1(C-4)飛彈,射程為7400千米,裝有8個分導式多彈頭,命中精度約...
北約在沉寂了10年之後,於2015年10月3日至11月6日舉行了號稱是歷史上最適應現代戰爭的、2002年以來規模最大的代號為“三叉戟接點”的陸海空聯合作戰演習,來自...
海神三叉戟,是海神的武器,《斗羅大陸》主角唐三於二百五十三章《拔出,神器,海神的三叉戟》得到的神器,在唐三手裡只有一百零八斤,對外界來說重達十萬八千斤,...
波塞冬三叉戟(Trident of Poseidon)是奧林匹斯海神波塞冬的武器,海王也曾短暫使用過它。...
北約“三叉戟接點2018”聯合軍事演習於2018年10月25日至11月7日舉行,這是北約自冷戰結束以來規模最大的一次聯合軍演。...
上海三叉戟信息科技有限公司於2010年6月24日在閔行區市場監督管理局登記成立。法定代表人張劍福,公司經營範圍包括計算機軟硬體、網路通訊產品領域內的技術開發等。...
三叉戟2型飛彈(UGM-133 Trident-II,或稱 Trident D5)是美國海軍第三代潛地彈道飛彈。三叉戟2型彈道飛彈現系美國海軍最重要的海基核威懾力量,或稱三叉戟D5飛彈...
三叉戟(呂錚長篇小說)編輯 鎖定 金盾文學獎獲得者呂錚全新力作。 再現公安幹警面對情理法的複雜糾葛與人性抉擇,揭露情義、法制、理念、信仰的糾葛與較量。被馮小剛...
1971年10月起預研,1976年12月起投產,1977年1月進行首次飛行試驗,1979年10月後裝備12艘改裝拉斐特級飛彈核潛艇,每艇16枚三叉戟Ⅰ飛彈;另一部分裝備3艘新的...
TRIDENT(瑞典三叉戟國際釣具) 瑞典三叉戟國際釣具公司是一家歷史悠久的戶外運動產品的專業研發、生產和銷售的公司。產品系列主要有漁桿、漁輪、漁線、假餌、漁具盒、...
戈博銀色三叉戟,銀色三叉戟的名字來自海豹部隊的資格章 - 大家喜歡叫它“三叉戟”。現在海豹部隊的的三叉戟是金色的,但以前的海豹資格章是銀色的,所以這把刀被...
三叉戟,是遊戲《Q寵大樂斗》的武器。...... 三叉戟,是遊戲《Q寵大樂斗》的武器。中文名 三叉戟 武器類型 大型 傷害 25-50 來源 Q寵大樂斗的武器 目錄 1...
UGM-133A彈道飛彈(代號:UGM-133A,名稱:Trident II,譯文:三叉戟II型,又稱:三叉戟D5),是美國海軍第三代潛地彈道飛彈。UGM-133A彈道飛彈是美國海軍最重要的...
