三代角定理

三代角定理用來計算在一個母角角度在360以內的角均分成N份（N可以非整數）後，得到N個子角，然後在該母角以及每個子角上做弦，其各個（子角的弦或者弦延長線）與（母角的弦或者延長線）自然相交的角度，這裡稱這種角為孫角。

基本介紹

• 中文名：三代角定理
• 公式：z*(n/2+0.5-t)=m*(n/2+0.5-t)/n
• z ：子角的度數
• n ：把母角分成多少等份
• 發現者：朱雄亮

公式

St =z*(n/2+0.5-t)=m*(n/2+0.5-t)/n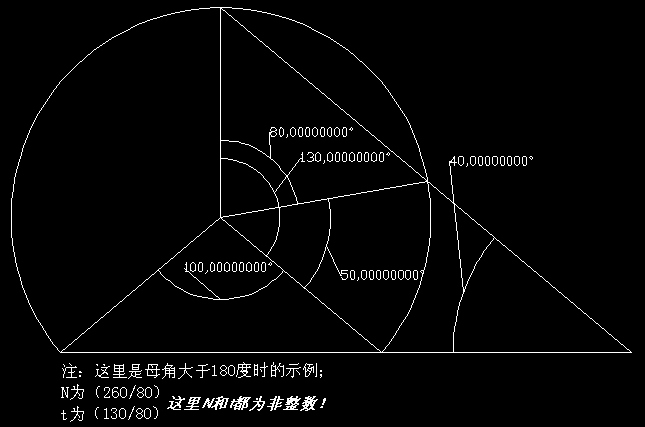

大於180度角所產生的孫角照樣適用本定理

公式中各表示為：

St —— 第幾個孫角的角度

z —— 子角的度數

* —— 數學算式中的乘法運算符號

n —— 把母角分成多少等份

/ —— 數學運算符號中的除法運算符號

2 —— 數字2

+ —— 數學運算符號中的加法運算符號

0.5 ——數值0.5

- —— 數學運算符號中的減法運算符號

t ——第幾個孫角

m —— 母角的角度

註：公式中：N可以非整數，t也可以非整數！

示例

如圖所示：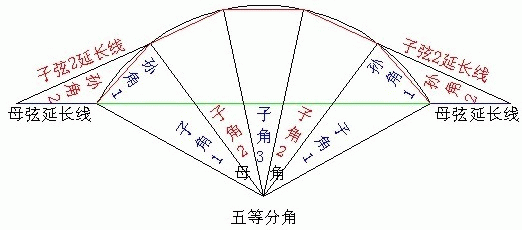

五等分角示例

把一個母角均分成5等份後，得到5個角度相同的子角（兩個子角1、兩個子角2、一個子角3，）；在每個子角上做弦（圖中紅色的線）和母角上做弦（圖中綠色的線），並且讓各子角弦與母角弦自然相交（如不能相交，做各自的延長線（圖中有提示的黑色的線），直至相交為止（子角份數分為奇份數的，中間那條子弦與母弦不能相交，因為它們是處於平行狀態！但仍遵守這個定理））；這樣這個示例中就產生了4個孫角，它們的各個角度可以用上面的定理，把各變數代進去，就可以把各個孫角的角度給計算出來！

註：（這個示例因為是把母角均分成5份，為奇份數，所以中間那個孫角的角度為0度，所以這個示例只有4個孫角；如果母角的均分份數為偶份數（如6份），那么就有產生6個孫角了！如圖：）這個定理可以把360度以內的母角均分成任意份數，計算其子弦與母弦相交產生的各個孫角角度！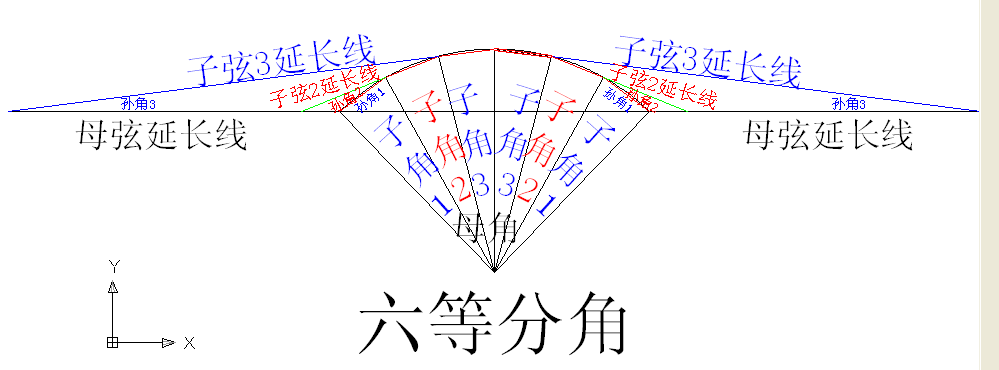

六等分角

發現者：中華人民共和國浙江省麗水市縉雲縣五雲鎮洋潭頭村（原項山村）：朱雄亮

發現時間：2000年9月12日

發表時間：2011年3月18日