一般點是近代(19世紀末至今)代數幾何的一個基本概念。在概形理論中,一般點的定義略有不同。一個仿射概形的一個一般點指的是 R 的一個極小素理想,而一個概形的一般點指的是它的所有仿射開子概形的一般點全體。
基本介紹
- 中文名:一般點
- 外文名:generic point
- 適用範圍:數理科學
定義
例證法
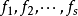
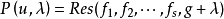
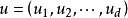
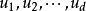
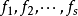
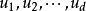
一般點是近代(19世紀末至今)代數幾何的一個基本概念。在概形理論中,一般點的定義略有不同。一個仿射概形的一個一般點指的是 R 的一個極小素理想,而一個概形的一般點指的是它的所有仿射開子概形的一般點全體。
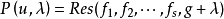
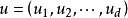
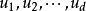
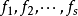
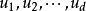
一般點是近代(19世紀末至今)代數幾何的一個基本概念。在概形理論中,一般點的定義略有不同。一個仿射概形的一個一般點指的是 R 的一個極小素理想,而一個概...
一般性勘探點 exploratory hole 為查明地基主要受力層性質,滿足地基(包括樁基)承載力評價等一般常規性問題的要求而布設的勘探點。 ...
一般是一個漢語辭彙,讀音為yì bān,是指一樣,普通,總體上,相關文獻有唐王建《宮詞》。一般的近義詞為普通,若干,反義詞為特別。...
一般式是關於直線的一個方程,在直角坐標系下,我們把關於x,y的方程Ax+By+C=0(A、B不能同時等於0)叫做直線的一般式方程,簡稱一般式。另外,二次函式也有它的...
一般辭彙是相對於基本辭彙而言,在一種語言辭彙系統中,除去基本辭彙以外的一般辭彙,包括固定詞組。一般辭彙是一般詞的總和,具有變化迅速,缺少歷史穩固性的基本特點。...
一般件是指除關鍵件以外的其他機械備件。...... 一般件按零件交貨期的先後進行排序,並制定每周的零件投產計畫。[1] 一般件的特點是:多數零件的工序數少,加工勞動...
對三個投影面無平行、垂直關係,而對三個投影面都傾斜的直線稱為一般位置直線。直線與H,V,W三個投影面的夾角一般分別用α,β,γ表示。一般位置直線的各投影與...
一般代理是指不享有獨家代理專營權的代理,即委託人在同一地區和期限內,對同一商品可同時委託幾個代理人代表委託人的行為。一般代理根據推銷商品的實際金額和根據...
《一般知識》是一款Android平台的套用。...... 《一般知識》是一款Android平台的套用。 軟體名稱 一般知識 軟體平台 Android 軟體大小 2.17M ...
這是大家比較容易忽視的一點,我們都清楚排名前1-3位點擊流量比較大,但同行調低...前幾位的價錢一般都很高,很容易成為欺詐點擊的對象,所以我們採取比較合理的排名,...
我國高層建築樓房一般分為“板式樓”和“點式樓”兩種。點式樓一般是高層,以電梯為中心,圍繞著很多戶型,朝北、朝南、朝東、朝西的都有,所以有部分戶型終年不見...
水準點(Benchmark,簡稱BM)是用水準測定高程的點。為了滿足工程建設的需要,測繪部門已在全國各地測定了許多水準點。在水準測量之前應做好點的標誌。水準點一般分為...
生長點,植物學上通常稱為分生區,又稱生長錐或頂端分生組織,此處細胞分裂活動旺盛。根和莖的頂端分生組織又叫生長點或生長錐,植物學一般稱之為分生區。分生區...
