Θ函式

數學中，Θ函式是一種多復變特殊函式。其套用包括阿貝爾簇與模空間、二次形式、孤立子理論；其格拉斯曼代數推廣亦出現於量子場論，尤其於超弦與D-膜理論。Θ函式最常見於橢圓函式理論。相對於其“z” 變數，Θ函式是擬周期函式（quasiperiodic function），具有“擬周期性”。在一般下降理論（descent theory）中，此來自線叢條件。

基本介紹

• 中文名：Θ函式
• 分類：模形式、黎曼曲面
• 套用：橢圓函式
• 領域：數理科學

雅可比Θ函式

雅可比Θ函式取二變數 與 ，其中 為任何複數，而 為上半複平面上一點；此函式之定義為：

若固定 ，則此成為一周期為1的單變數 整函式的傅立葉級數：

在以 位移時，此函式符合：

其中a與b為整數。

輔助函式

可定義輔助函式：

其中符號依黎曼與芒福德之習慣；雅可比的原文用變數 替換了 ，而稱本條目中的Θ為 為 為 為 。

若設 ，則我們可從以上獲得四支單以 ，為變數之函式，其中 ,取值於上半複平面。此等函式人稱“Θ‘常量’”（theta constant）；我們可以用Θ函式定義一系列模形式，或參數化某些曲線。由“雅可比 恆等式”可得：

是為四次費馬曲線。

雅可比恆等式

雅可比恆等式描述模群在Θ函式之作用；模群之生成元為T: τ ↦ τ+1與S: τ ↦ -1/τ。我們已有 T 作用之式。設：

則

以nome q表示Θ函式

我們可用變數 與 ，代替 與 ，來表示ϑ。設 而 。則ϑ可表示為：

而輔助Θ函式可表示為：

此表示式不需要指數函式，所以適用於指數函式無每一處定義域，如p進數域。

乘積表示式

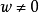雅可比三重積恆等式（Jacobi's triple product identity）中指出：若有複數 與 ，其中 而 ，則

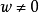
此式可以用基本方法證明，如戈弗雷·哈羅德·哈代和愛德華·梅特蘭·賴特共同編著的《數論導引》。

若用nome變數與表示，則有：

由此得到Θ函式的積公式：

三重積等式左邊可以擴展成：

即：

這個式子在z取實值時尤為重要。 各輔助Θ函式亦有類似之積公式：

積分表示式

雅可比Θ函式可用積分表示，如下：

與黎曼ζ函式的關係

黎曼嘗用關係式

以證黎曼ζ函式之函式方程。他寫下等式：

而此積分於替換 下不變。z非零時之積分，在赫爾維茨ζ函式一文有描述。

與維爾斯特拉斯橢圓函式之關係

雅可比用Θ函式來構造橢圓函式，並使其有易於計算之形式。他表示他的橢圓函式成兩枚上述Θ函式之商。魏爾施特拉斯橢圓函式亦可由雅可比Θ構造：

其中二次微分相對於z，而常數c使的羅朗級數（於 z = 0）常項為零。

與模形式之關係

設η為戴德金η函式。則

解熱方程

雅可比Θ函式為一維熱方程、於時間為零時符合周期邊界條件之唯一解。 設z = x取實值，τ = it而t取正值。則有

此解此下方程：

於t = 0時，Θ函式成為“狄拉克梳狀函式”（Dirac comb）

其中δ為狄拉克δ函式，故可知此解是唯一的。 因此，一般解可得自t = 0時的（周期）邊界條件與Θ函式的卷積。

與海森堡群之關係

雅可比Θ函在海森堡群之一離散子群作用下不變。見海森堡群之Θ表示一文。

推廣

若F為一n元二次型，則有一關連的Θ函式

其中為整數格。此Θ函式是模群（或某適當子群）上的權n/2 模形式。在其富理埃級數

中，稱為此模形式之“表示數”（representation numbers）。