基本介紹
- 中文名:softmax邏輯回歸
- 外文名:Softmax logical regression
簡介,代價函式,Softmax回歸模型參數化的特點,權重衰減,Softmax回歸與Logistic 回歸的關係,Softmax 回歸 vs. k 個二元分類器,中英文對照,
簡介
在 logistic 回歸中,我們的訓練集由m個已標記的樣本構成: ,其中輸入特徵
,其中輸入特徵 。(我們對符號的約定如下:特徵向量x的維度為n+1,其中
。(我們對符號的約定如下:特徵向量x的維度為n+1,其中 對應截距項 。) 由於 logistic 回歸是針對二分類問題的,因此類標記
對應截距項 。) 由於 logistic 回歸是針對二分類問題的,因此類標記 。假設函式(hypothesis function) 如下:
。假設函式(hypothesis function) 如下:





我們將訓練模型參數 ,使其能夠最小化代價函式 :
,使其能夠最小化代價函式 :







對於給定的測試輸入 ,我們想用假設函式針對每一個類別j估算出機率值
,我們想用假設函式針對每一個類別j估算出機率值 。也就是說,我們想估計
。也就是說,我們想估計 的每一種分類結果出現的機率。因此,我們的假設函式將要輸出一個
的每一種分類結果出現的機率。因此,我們的假設函式將要輸出一個 維的向量(向量元素的和為1)來表示這
維的向量(向量元素的和為1)來表示這 個估計的機率值。 具體地說,我們的假設函式
個估計的機率值。 具體地說,我們的假設函式 形式如下:
形式如下:







其中 是模型的參數。請注意
是模型的參數。請注意 這一項對機率分布進行歸一化,使得所有機率之和為 1 。
這一項對機率分布進行歸一化,使得所有機率之和為 1 。


為了方便起見,我們同樣使用符號 來表示全部的模型參數。在實現Softmax回歸時,將
來表示全部的模型參數。在實現Softmax回歸時,將 用一個
用一個 的矩陣來表示會很方便,該矩陣是將
的矩陣來表示會很方便,該矩陣是將 按行羅列起來得到的,如下所示:
按行羅列起來得到的,如下所示:





代價函式
我們來介紹 softmax 回歸算法的代價函式。在下面的公式中,1是示性函式,其取值規則為:
1{值為真的表達式}=1
1{值為假的表達式} =0。舉例來說,表達式 的值為1 ,
的值為1 , 的值為 0。我們的代價函式為:
的值為 0。我們的代價函式為:



值得注意的是,上述公式是logistic回歸代價函式的推廣。logistic回歸代價函式可以改為:

可以看到,Softmax代價函式與logistic 代價函式在形式上非常類似,只是在Softmax損失函式中對類標記的 個可能值進行了累加。注意在Softmax回歸中將
個可能值進行了累加。注意在Softmax回歸中將 分類為類別
分類為類別 的機率為:
的機率為:




對於 的最小化問題,當前還沒有閉式解法。因此,我們使用疊代的最佳化算法(例如梯度下降法,或 L-BFGS)。經過求導,我們得到梯度公式如下:
的最小化問題,當前還沒有閉式解法。因此,我們使用疊代的最佳化算法(例如梯度下降法,或 L-BFGS)。經過求導,我們得到梯度公式如下:


讓我們來回顧一下符號 " " 的含義。
" 的含義。 本身是一個向量,它的第
本身是一個向量,它的第 個元素
個元素 是
是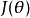 對
對 的第
的第 個分量的偏導數。
個分量的偏導數。




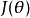


有了上面的偏導數公式以後,我們就可以將它代入到梯度下降法等算法中,來最小化 。 例如,在梯度下降法的標準實現中,每一次疊代需要進行如下更新:
。 例如,在梯度下降法的標準實現中,每一次疊代需要進行如下更新: (
( )。
)。



當實現 softmax 回歸算法時, 我們通常會使用上述代價函式的一個改進版本。具體來說,就是和權重衰減(weight decay)一起使用。我們接下來介紹使用它的動機和細節。
Softmax回歸模型參數化的特點
Softmax 回歸有一個不尋常的特點:它有一個“冗餘”的參數集。為了便於闡述這一特點,假設我們從參數向量 中減去了向量
中減去了向量 ,這時,每一個
,這時,每一個 都變成了
都變成了 (
(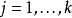 )。此時假設函式變成了以下的式子:
)。此時假設函式變成了以下的式子:




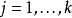

換句話說,從 中減去
中減去 完全不影響假設函式的預測結果!這表明前面的 softmax 回歸模型中存在冗餘的參數。更正式一點來說, Softmax 模型被過度參數化了。對於任意一個用於擬合數據的假設函式,可以求出多組參數值,這些參數得到的是完全相同的假設函式
完全不影響假設函式的預測結果!這表明前面的 softmax 回歸模型中存在冗餘的參數。更正式一點來說, Softmax 模型被過度參數化了。對於任意一個用於擬合數據的假設函式,可以求出多組參數值,這些參數得到的是完全相同的假設函式 。
。



進一步而言,如果參數 是代價函式
是代價函式 的極小值點,那么
的極小值點,那么 同樣也是它的極小值點,其中
同樣也是它的極小值點,其中 可以為任意向量。因此使
可以為任意向量。因此使 最小化的解不是獨立的。(有趣的是,由於
最小化的解不是獨立的。(有趣的是,由於 仍然是一個凸函式,因此梯度下降時不會遇到局部最優解的問題。但是 Hessian 矩陣是奇異的不可逆的,這會直接導致採用牛頓法最佳化就遇到數值計算的問題)
仍然是一個凸函式,因此梯度下降時不會遇到局部最優解的問題。但是 Hessian 矩陣是奇異的不可逆的,這會直接導致採用牛頓法最佳化就遇到數值計算的問題)






注意,當 時,我們總是可以將
時,我們總是可以將 替換為
替換為 (即替換為全零向量),並且這種變換不會影響假設函式。因此我們可以去掉參數向量
(即替換為全零向量),並且這種變換不會影響假設函式。因此我們可以去掉參數向量 (或者其他
(或者其他 中的任意一個)而不影響假設函式的表達能力。實際上,與其最佳化全部的
中的任意一個)而不影響假設函式的表達能力。實際上,與其最佳化全部的 個參數
個參數 (其中
(其中 ),我們可以令
),我們可以令 ,只最佳化剩餘的
,只最佳化剩餘的  個參數,這樣算法依然能夠正常工作。
個參數,這樣算法依然能夠正常工作。










在實際套用中,為了使算法實現更簡單清楚,往往保留所有參數 ,而不任意地將某一參數設定為 0。但此時我們需要對代價函式做一個改動:加入權重衰減。權重衰減可以解決 softmax 回歸的參數冗餘所帶來的數值問題。
,而不任意地將某一參數設定為 0。但此時我們需要對代價函式做一個改動:加入權重衰減。權重衰減可以解決 softmax 回歸的參數冗餘所帶來的數值問題。

權重衰減
我們通過添加一個權重衰減項 來修改代價函式,這個衰減項會懲罰過大的參數值,我們的代價函式變為:
來修改代價函式,這個衰減項會懲罰過大的參數值,我們的代價函式變為:


有了這個權重衰減項以後 (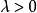 ),代價函式就變成了嚴格的凸函式,這樣就可以保證得到獨立的解了。 此時的 Hessian矩陣變為可逆矩陣,並且因為
),代價函式就變成了嚴格的凸函式,這樣就可以保證得到獨立的解了。 此時的 Hessian矩陣變為可逆矩陣,並且因為 是凸函式,梯度下降法和 L-BFGS 等算法可以保證收斂到全局最優解。
是凸函式,梯度下降法和 L-BFGS 等算法可以保證收斂到全局最優解。
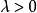

為了使用最佳化算法,我們需要求得這個新函式 的導數,如下:
的導數,如下:


通過最小化 ,我們就能實現一個可用的 softmax 回歸模型。
,我們就能實現一個可用的 softmax 回歸模型。

Softmax回歸與Logistic 回歸的關係
當類別數 時,softmax 回歸退化為 logistic 回歸。這表明 softmax 回歸是 logistic 回歸的一般形式。具體地說,當
時,softmax 回歸退化為 logistic 回歸。這表明 softmax 回歸是 logistic 回歸的一般形式。具體地說,當 時,softmax 回歸的假設函式為:
時,softmax 回歸的假設函式為:



利用softmax回歸參數冗餘的特點,我們令 ,並且從兩個參數向量中都減去向量
,並且從兩個參數向量中都減去向量 ,得到:
,得到:



因此,用 來表示
來表示 ,我們就會發現 softmax 回歸器預測其中一個類別的機率為
,我們就會發現 softmax 回歸器預測其中一個類別的機率為 ,另一個類別機率的為
,另一個類別機率的為 ,這與 logistic回歸是一致的。
,這與 logistic回歸是一致的。




Softmax 回歸 vs. k 個二元分類器
如果你在開發一個音樂分類的套用,需要對k種類型的音樂進行識別,那么是選擇使用 softmax 分類器呢,還是使用 logistic 回歸算法建立 k 個獨立的二元分類器呢?
這一選擇取決於你的類別之間是否互斥,例如,如果你有四個類別的音樂,分別為:古典音樂、鄉村音樂、搖滾樂和爵士樂,那么你可以假設每個訓練樣本只會被打上一個標籤(即:一首歌只能屬於這四種音樂類型的其中一種),此時你應該使用類別數k= 4的softmax回歸。(如果在你的數據集中,有的歌曲不屬於以上四類的其中任何一類,那么你可以添加一個“其他類”,並將類別數k設為5。)
如果你的四個類別如下:人聲音樂、舞曲、影視原聲、流行歌曲,那么這些類別之間並不是互斥的。例如:一首歌曲可以來源於影視原聲,同時也包含人聲 。這種情況下,使用4個二分類的 logistic 回歸分類器更為合適。這樣,對於每個新的音樂作品 ,我們的算法可以分別判斷它是否屬於各個類別。
當前我們來看一個計算視覺領域的例子,你的任務是將圖像分到三個不同類別中。(i) 假設這三個類別分別是:室內場景、戶外城區場景、戶外荒野場景。你會使用sofmax回歸還是 3個logistic 回歸分類器呢? (ii) 當前假設這三個類別分別是室內場景、黑白圖片、包含人物的圖片,你又會選擇 softmax 回歸還是多個 logistic 回歸分類器呢?
在第一個例子中,三個類別是互斥的,因此更適於選擇softmax回歸分類器 。而在第二個例子中,建立三個獨立的 logistic回歸分類器更加合適。
中英文對照
- Softmax回歸 Softmax Regression
- 有監督學習 supervised learning
- 無監督學習 unsupervised learning
- 深度學習 deep learning
- logistic回歸 logistic regression
- 截距項 intercept term
- 二元分類 binary classification
- 類型標記 class labels
- 估值函式/估計值 hypothesis
- 代價函式 cost function
- 多元分類 multi-class classification
- 權重衰減 weight decay

