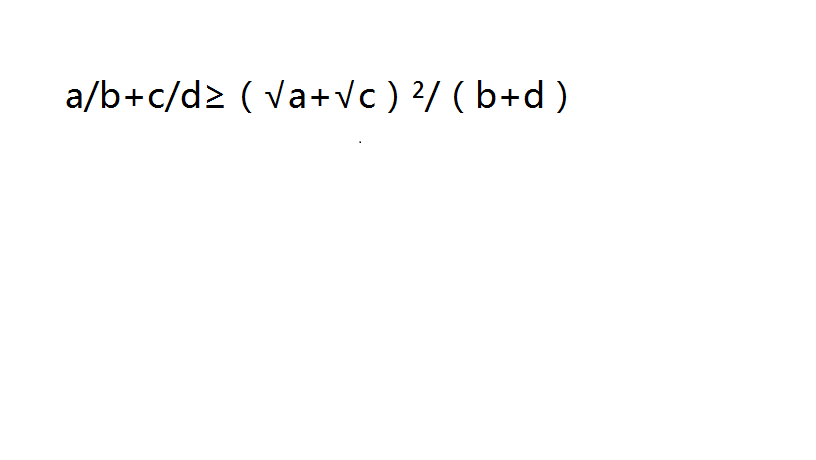在高中數學學習中,除了日常的絕對值不等式和基本不等式外,在解決已知x與y關係,求關於x,y分式問題時,可以運用hxq不等式。
hxq不等式的基本形式為a/b+c/d≥(√a+√c)2/(b+d)。
若且唯若ad2=cb2時成立
其中a,b,c,d均大於0
基本介紹
- 中文名:hxq不等式
- 外文名:hxq-inequality
- 別稱:分母求和不等式/分子根方不等式
- 表達式:a/b+c/d≥(√a+√c)2/(b+d)
- 提出者:黃顯強
- 提出時間:2015.4.29
- 套用學科:數學
- 適用領域範圍:已知x與y關係,求關於x,y分式問題
證明
已知a/b+c/d
則添加式子(a/b+c/d)(b+d)/(b+d)
化簡得 (a+c+ad/b+bc/d)/(b+d)
運用基本不等式
(a+c+ad/b+ad/b)/(b+d)≥(a+c+2√(ad/b*bc/d))/(b+d)
=(a+c+2√ab)(b+d)=(√a+√c)2/(b+d)
綜上所述,證得hxq不等式
a/b+c/d≥(√a+√c)2/(b+d)其中a,b,c,d均大於0且b+d≠0
套用
第一類簡單題
x,y是正數,x+3y=2,1/x+1/y的最小值
基本不等式法(x+3y)(1/x+1/y)=1+3y/x+x/y+3=4+(3y/x+x/y)≥4+2√[(3y/x)(x/y)]=4+2√3
因為x+3y=2所以2(1/x+1/y)≥4+2√31/x+1/y≥2+√31/x+1/y的最小值是2+√3
hxq不等式法 1/x+1/y=1/x+3/3y≥(√1+√3)2/(x+3y)=(4+2√3)/2=2+√3
第二類麻煩題
已知x>y>0 x+y≤2 求2/(x+3y) +1/(x-y)最小值
基本不等式法
x>y>0且x+y≤2,
故依均值不等式得
2/(x+3y)+1/(x-y)
=1·[2/(x+3y)+1/(x-y)]
=[(x+3y)+(x-y)]/4·[2/(x+3y)+1/(x-y)]
=3/4+(1/4)·[(x+3y)/(x-y)+2(x-y)/(x+3y)]
≥3/4+(1/4)·2√[(x+3y)/(x-y)·2(x-y)/(x+3y)]
=(3+2√2)/4.
∴(x+3y)/(x-y)=2(x-y)/(x+3y)且x+y=2
即x=-1+2√2,y=3-2√2時,
所求最小值為: (3+2√2)/4。
故依均值不等式得
2/(x+3y)+1/(x-y)
=1·[2/(x+3y)+1/(x-y)]
=[(x+3y)+(x-y)]/4·[2/(x+3y)+1/(x-y)]
=3/4+(1/4)·[(x+3y)/(x-y)+2(x-y)/(x+3y)]
≥3/4+(1/4)·2√[(x+3y)/(x-y)·2(x-y)/(x+3y)]
=(3+2√2)/4.
∴(x+3y)/(x-y)=2(x-y)/(x+3y)且x+y=2
即x=-1+2√2,y=3-2√2時,
所求最小值為: (3+2√2)/4。
hxq不等式法2/(x+3y)+1/(x-y)≥(√2+1)2/(2x+2y)≥(3+2√2)/4(由x+y≤2得來)
所求最小值為(3+2√2)/4。
總結
在已知x,y關係 求關於求關於x,y分式問題時,可以運用hxq不等式便於求解。
例題√(12-3t)+√t的最大值
可以用hxq不等式的另一邊
即√a+√c≤√(a/b+c/d)(b+d)
帶入數據
即√(12-3t)+√t≤√((12-3t)/b+t/d)(b+d)
根據不等式一正二定原則
消去變數t 使b=3,d=1(b,d任意取值使t消去)
此時√(12-3t)+√t≤√((12-3t)/b+t/d)(b+d)=√((12-3t)/3+t/1)(3+1)=√4*4=4
因此√(12-3t)+√t最大值為4.
總結在基本不等式無法消去變數求最大值時,可以用hxq不等式便於求解
hxq猜想
在分式中,分子分母均為正實數,那么任何幾項數之和,大於等於其分子算數平方根之和的平方除以其分母之和
即a/b+c/d+e/f+.....+x/y≥(√a+√c+√e+.....+√x)2/(b+d+f+.....+y)
在hxq猜想成立後,可用以求分式數列和不等式問題。