ChaCha20-Poly1305是Google所採用的一種新式加密算法，性能強大，在CPU為精簡指令集的ARM平台上尤為顯著（ARM v8前效果較明顯），在同等配置的手機中表現是AES的4倍（ARM v8之後加入了AES指令，所以在這些平台上的設備，AES方式反而比chacha20-Poly1305方式更快，性能更好），可減少加密解密所產生的數據量進而可以改善用戶體驗，減少等待時間，節省電池壽命等。谷歌選擇了ChaCha20和伯恩斯坦的Poly1305訊息認證碼取代過去一直在網際網路安全領域使用的基於OpenSSL的RC4密碼，谷歌最初是為了保證能夠在Android手機上的Chrome瀏覽器和谷歌網站間的HTTPS（TLS/SSL）通訊。在谷歌採用TLS（安全傳輸層協定）不久後，ChaCha20和Poly1305均用在OpenSSH中的ChaCha20-Poly1305新算法中，這使得OpenSSH可能避免因編譯時間對OpenSSL產生依賴。ChaCha20還用於OpenBSD（一種多平台類UNIX作業系統）中的RC4隨機數生成器，在DragonFlyBSD中作為核心的偽隨機數產生器（Cryptographically Secure Pseudo-Random Number Generator，簡稱CSPRNG）的子程式。
基本介紹
- 中文名：ChaCha20-Poly1305
- 外文名：ChaCha20-Poly1305
- 設計者：Daniel J. Bernstein
- 提出時間：2014年
- 套用學科：密碼學
- 適用領域範圍：計算機、網際網路、安全協定
- 算法結構：AEAD（MtE）關聯數據認證加密
算法簡介,設計者,算法介紹,標準化,
算法簡介
ChaCha20-Poly1305是由ChaCha20流密碼和Poly1305訊息認證碼（MAC）結合的一種套用在網際網路安全協定中的認證加密算法，由Google公司率先在Andriod移動平台中的Chrome中代替RC4使用。由於其算法精簡、安全性強、兼容性強等特點，目前Google致力於全面將其在移動端推廣。
設計者
Daniel J. Bernstein教授，德裔美籍數學家、密碼學家、程式設計師。Eindhoven University of Technology的數學與計算機教授，設計了salsa、chacha等著名的流密碼算法和Poly1305訊息認證碼，對國際密碼學界影響深遠。
算法介紹
ChaCha20
ChaCha系列流密碼，作為salsa密碼的改良版，具有更強的抵抗密碼分析攻擊的特性，“20”表示該算法有20輪的加密計算。
由於是流密碼，故以位元組為單位進行加密，安全性的關鍵體現在密鑰流生成的過程，即所依賴的偽隨機數生成器（PRNG）的強度，加密過程即是將密鑰流與明文逐位元組異或得到密文，反之，解密是將密文再與密鑰流做一次異或運算得到明文。
算法過程：
（1）ChaCha20的初始矩陣
ChaCha20有一個初始矩陣，矩陣的輸入為一個256位的密鑰、64位隨機數、64位計數器值以及4×32位的常數，它們均填充在32位整型數組中作為初始矩陣。排列方式如下。
0x61707865 0x3320646e 0x79622d32 0x6b206574
Key[0] Key[1] Key[2] Key[3]
Key[4] Key[5] Key[6] Key[7]
Counter[0] Counter[1] nonce[0] nonce[1]
這裡256位密鑰即流密碼的初始密鑰，常數為通信雙方在握手協定中協商的定值，計數器值取一個從0開始每次自增1的暫存器（64位）中的值，隨機數為偽隨機數生成器產生，每次生成密鑰矩陣時產生不同的隨機數。
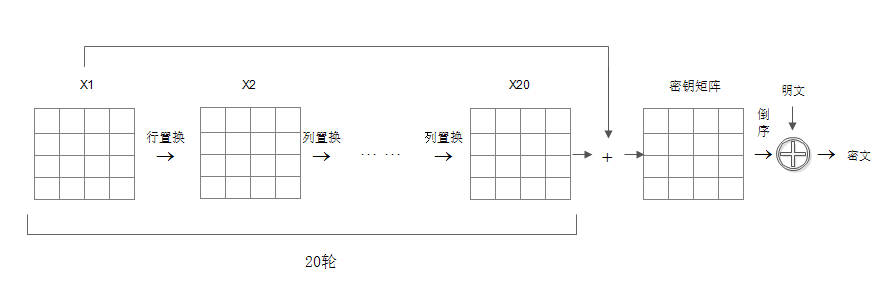
（2）初始矩陣置換
ChaCha20算法有20輪運算，其中奇數輪次與偶數輪次在執行輪函式前需要分別經過行置換和列置換，故20輪運算可以看作10次疊代，每次疊代先做行置換再做列置換，具體置換方法如下：
我們將初始矩陣存儲在一個4×4的數組X中，數組編號從0到15，初始矩陣表示為：
X[0]，X[1]，X[2]，X[3]，
X[4]，X[5]，X[6]，X[7],
X[8]，X[9]，X[A]，X[B]，
X[C]，X[D]，X[E]，X[F]
經過行置換（奇次）後：
X[0]，X[4]，X[8]，X[C]，
X[1]，X[5]，X[9]，X[D]，
X[2]，X[6]，X[A]，X[E]，
X[3]，X[7]，X[B]，X[F]
經過列置換（偶次）後：
X[0]，X[5]，X[A]，X[F]，
X[1]，X[6]，X[B]，X[C]，
X[2]，X[7]，X[8]，X[D]，
X[3]，X[4]，X[9]，X[E]
（3）輪函式
在矩陣每次完成置換後，都需要執行一次輪函式QUARTERROUND，該函式輸入為4個32位串，即4個數組中的元素，輸出同樣也為4個32位串，這樣執行完輪函式後除了數據以外，矩陣結構未發生任何變化，這裡拿第一次行置換後的矩陣執行輪函式舉例，執行輪函式操作如下。
QUARTERROUND（X[0]，X[4]，X[8]，X[C]）；
QUARTERROUND（X[1]，X[5]，X[9]，X[D]）；
QUARTERROUND（X[2]，X[6]，X[A]，X[E]）；
QUARTERROUND（X[3]，X[7]，X[B]，X[F]）；
輪函式具體實施步驟，這裡我令輪函式4個輸入分別是a，b，c，d，經過一系列變換後得到輸出a，b，c，d（更新後的），過程如下：
a+=b；d^=a；d<<<16；
c+=d；b^=c；b<<<12；
a+=b；d^=a；d<<<8；
c+=d；b^=c；b<<<7；
這裡“+”是按位邏輯加，“^”是按位異或，“<<<”是循環左移。經過輪函式變換後得到一個新的矩陣，新矩陣再進行列置換，然後在執行輪函式，到此，初始矩陣已經執行過一次行置換、一次列置換以及兩次輪函式，完成了一輪疊代即兩個周期。
關於輪函數裡的計算操作，舉個例子，這裡令a=0x 11111111，b=0x 01020304，
c=0x 77777777，d=0x 01234567，然後我們分別執行“+”“^”“<<<”運算如下：
c=c+d=0x 77777777+0x 01234567=0x 789abcde；
b=b^c=0x 01020304^0x 789abcde=0x 7998bfda;
b=b<<<7=0x 7998bfda<<<7=0x cc5fed3c;
（4）生成密鑰流
在經過輪函式20輪周期（10輪行周期+10輪列周期）後，初始矩陣已經變成了一個新的4×4矩陣，此時將新矩陣與初始矩陣矢量相加，得到的矩陣再拆分倒序序列化處理後即得到一個512位的密鑰比特流。
（5）加密
將需要加密的信息（明文）與密鑰流按位異或即得到密文，當明文大於512位時，按照上述步驟依次生成密鑰流，由於計數器是32位，理論上可以生成
2 ^ 512 bit（256GB）的密鑰流，所以一般長度的信息加密完全足夠。
（6）解密
接收方使用傳送方傳輸過來的初始密鑰、隨機數以及協商好的常數和依次遞增的計數器值按照ChaCha20的密鑰流生成規則產生與加密相同的密鑰流，按位與密文異或即可得到明文。
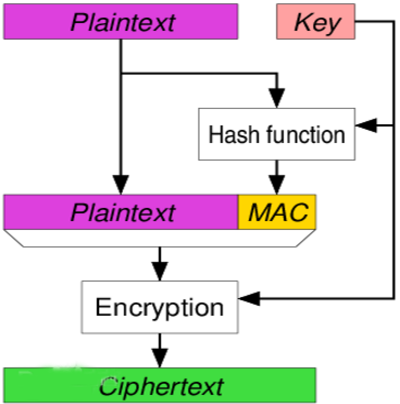
Poly1305訊息認證碼
訊息認證碼（帶密鑰的Hash函式）:密碼學中，通信實體雙方使用的一種驗證機制，保證訊息數據完整性的一種工具。構造方法由M.Bellare提出，安全性依賴於Hash函式，故也稱帶密鑰的Hash函式。訊息認證碼是基於密鑰和訊息摘要所獲得的一個值，可用於數據源發認證和完整性校驗。
Poly1305是Daniel.J.Bernstein創建的訊息認證碼，可用於檢測訊息的完整性和驗證訊息的真實性，現常在網路安全協定（SSL/TLS）中與salsa20或ChaCha20流密碼結合使用。
Poly1305訊息認證碼的輸入為32位元組（256bit）的密鑰和任意長度的訊息比特流，經過一系列計算生成16位元組（128bit）的摘要。算法的具體實施步驟如下。
（1） 密鑰處理
首先將32位元組的密鑰分成16位元組的兩組，前16位元組稱作“r”，後16位元組稱作“s”，申請兩個大小為16的數組r[]和s[]，對於s，將其以位元組為單位，倒序排列，即s[0]=s[15],s[1]=s[14],……,s[15]=s[0]（“=”前後的s[]為兩個數組）：
這裡假設s=01:03:80:8a:fb:0d:b2:fd:4a:bf:f6:af:41:49:f5:1b
倒序排列後s=1bf54941aff6bf4afdb20dfb8a800301（這裡去掉分組號， 形成比特流）。
對於r，將r[3],r[7],r[11],r[15]前4位清零（使其小於16），r[4],r[8],r[12]最後兩位清零（能夠被4整除），前4位清零操作可以通過與00001111邏輯乘得到，後2位清零可以通過與11111100邏輯乘得到，完成清零操作後，類似於s一樣對r進行按位元組倒序排列：
這裡假設r=85:d6:be:78:57:55:6d:33:7f:44:52:fe:42:d5:06:a8
清零操作後r=85:d6:be:08:54:55:6d:03:7c:44:52:0e:40:d5:06:08
倒序排列後r=806d5400e52447c036d555408bed685
（2） 加密函式
加密之前在系統中分配一個暫存器作為累加器ACC（程式中以數組表示），ACC初始值為0。
明文劃分為16位元組一組，這裡舉例假設明文如下：
000 43 72 79 70 74 6f 67 72 61 70 68 69 63 20 46 6f Cryptographic Fo
016 72 75 6d 20 52 65 73 65 61 72 63 68 20 47 72 6f rum Research Gro
032 75 70 up
（最左邊為序號，右邊部分為明文所對應的訊息內容）
明文這裡為34位元組，所以劃分為3組，其中最後一組只有2位元組，加密之前每組明文需要按位元組倒序排列（類似上文中密鑰的倒序排列操作），由於有3組明文，故加密需要3輪：
第一次加密：
ACC=00
Block（當前加密塊）=6f4620636968706172676f7470797243
在明文前加上字元串01：
Block with 0x01 byte = 016f4620636968706172676f7470797243
累加器值與當前加密塊值相加覆蓋累加器值（這裡是初始值00）：
Acc + Block = 016f4620636968706172676f7470797243
與密鑰r相乘
(Acc+Block) * r（806d5400e52447c036d555408bed685）=
b83fe991ca66800489155dcd69e8426ba2779453994ac90ed284034da565ecf
對常數P取余後將得到的值賦給ACC
Acc=(Acc+Block)*r)%P = 2c88c77849d64ae9147ddeb88e69c83fc
（P是常數2^130-5:3fffffffffffffffffffffffffffffffb,這裡的取余是為了讓ACC變成16.5位元組---132bit）
此時ACC中的值為第一輪加密後的結果
後面的加密模式和第一次相同，參與運算的為前一次運算結果（ACC中的值）和當前分組的明文。
第2、3次加密過程如下：
#2
Acc = 2c88c77849d64ae9147ddeb88e69c83fc
Block = 6f7247206863726165736552206d7572
Block with 0x01 byte = 016f7247206863726165736552206d7572
Acc + block = 437febea505c820f2ad5150db0709f96e
(Acc+Block) * r =
21dcc992d0c659ba4036f65bb7f88562ae59b32c2b3b8f7efc8b00f78e548a26
Acc=(Acc+Block)*r)%P = 2d8adaf23b0337fa7cccfb4ea344b30de
#3
Acc = 2d8adaf23b0337fa7cccfb4ea344b30de
Block = 7075
Block with 0x01 byte = 017075
Acc + block = 2d8adaf23b0337fa7cccfb4ea344ca153
(Acc + Block) * r =
16d8e08a0f3fe1de4fe4a15486aca7a270a29f1e6c849221e4a6798b8e45321f
((Acc + Block) * r) % P = 28d31b7caff946c77c8844335369d03a7
3輪加密後得到的ACC=28d31b7caff946c77c8844335369d03a7
將其與密鑰s相加（s=1bf54941aff6bf4afdb20dfb8a800301）：
Acc + s = 2a927010caf8b2bc2c6365130c11d06a8
可以發現ACC由於計算時附加01這半位元組的原因，一直都是16.5位元組，最後與s（16位元組）相加後仍為16.5位元組，此時將與s相加結果倒序排列後去掉最後半個位元組即得到16位元組的明文摘要：
Tag: a8:06:1d:c1:30:51:36:c6:c2:2b:8b:af:0c:01:27:a9
標準化
該算法的標準化文檔為RFC7539
