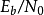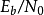定義
如果要編碼的信息可以被劃分成若干個k位二進制數字的塊,每個塊可以被編碼成n位二進制數字,那么這種編碼方式就是(n,k)- 塊碼。
 塊碼的結構
塊碼的結構更具體地,一個(n,k)-塊碼包含了一個編碼函式:
以及一個解碼函式:
碼字是E的值域中任意一個元素。 我們也要求E是一個一一映射的函式,這樣可以保證不存在兩個信息塊被映射到同一個碼字中。
背景
塊碼是早期通信系統系統中主要使用的信道編碼方式,創立塊碼的主要目的是希望能幫助用戶解決接收數據時任何可能的錯誤,而不需要聯繫數據的來源方。在編碼理論中,塊碼是以塊為單位編碼數據的一種編碼方式。 塊碼的概念使得編碼理論家,數學家和計算機科學家以統一的方式研究所有塊碼的限制。 這樣的限制通常採取將塊代碼的不同參數相互關聯的形式,例如其速率及其檢測和糾正錯誤的能力。
例子
美國數學家理察·漢明(Richard Hamming)在1950年為開創碼塊的過程中有著巨大的作用,因此有一種塊碼被命名為“漢明碼”。
此外還有一些常見的塊碼:Reed–Solomon碼,Hadamard 碼,Expander 碼,Golay 碼,Reed–Muller碼。這些編碼方式也屬於線性碼,更一般地這些編碼也被稱為代數塊碼,因為它們可以用布爾多項式生成。
塊碼的相關概念
字母Σ
要編碼的數據流被建模為一些
字母表上的
字元串 。尺寸
字母表經常寫為 q。如果q=2,則塊碼被稱為二進制塊碼。
訊息長度k
k稱為塊代碼的訊息長度或維度。
塊長度n
n稱為塊的長度。
漢明距離
兩個n比特二進制序列v1h和v2之間的漢明距離
就是v1和v2之間不同比特的個數。例如,假設v1=011011, v2=110001,那么
=3。
距離d
塊碼的距離(或最小距離)d是其中任何兩個不同的碼字的不同位置數的最小值,相對距離
是d/n。形式化地描述,塊碼C最小距離的定義是:
因為任何編碼的編碼函式都要求是單射的,所以任何編碼的最小距離至少是1。此外,距離還等於線性塊碼的最小權(碼字中1的個數),因為
冗餘度
冗餘比特與數據比特數的比率(n-k)/k稱為編碼的冗餘度。
編碼率
數據比特與總比特數的比率k/n稱為編碼率(code rate)。
流行的標記
代表著一種塊碼,它的字母表大小為q,塊的長度為n,訊息長度為k以及距離為d。如果分組碼是線性分組碼,則符號中的括弧就用方括弧表示
。對於q=2的二進制碼,下標往往會忽略。對於最大距離可分碼,距離永遠是
,但有時精確的距離是未知的、無法證明或表示,或不需要的,在這種情況下d這個成分往往會被忽略。
錯誤修正
碼字
可以被認為是一個n維度空間中的點和代碼 C是
子集 。C與(最小)距離 d 具有以下屬性:1、可以檢測 d-1 位錯誤。因為碼字之間的距離為d,所以如果發生1~d-1位的錯誤的話,接受到的編碼會不在C中,即檢測到錯誤。
 檢測錯誤位數說明
檢測錯誤位數說明2、可以糾(d-1)/2位錯。將d-1分開,對於落在兩個半區中的編碼,將其譯為最接近的碼字。因為碼字之間的距離為d所以解碼函式是一一映射的,即這種解碼方式是合法的。
3、如果要求同時糾正t個錯碼,同時檢測e個錯碼,那么最小碼距應為
。
例如,下圖中碼組A和B之間距離為5。按照檢錯能力公式,最多能檢測4個錯碼,即e = d – 1 = 5 – 1 = 4,按照糾錯能力公式糾錯時,能糾正2個錯碼。但是,不能同時作到兩者,因為當錯碼位數超過糾錯能力時,該碼組立即進入另一碼組的圓內而被錯誤地“糾正”了。例如,碼組A若錯了3位,就會被誤認為碼組B錯了2位造成的結果,從而被錯“糾”為B。這就是說,檢錯和糾錯公式不能同時成立或同時運用。
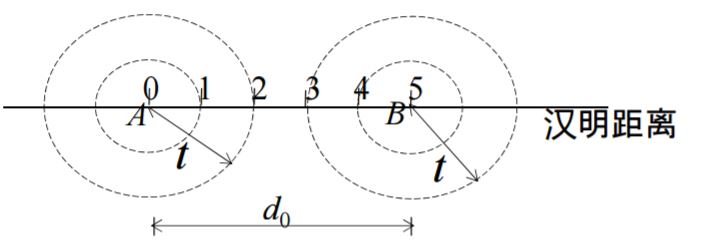 例子
例子對於塊碼我們一般採取最大似然解碼方式:將出現錯誤的碼字譯為距離它最近的碼字。
塊碼的上下界
編碼的族
被稱為編碼的族,其中
是
碼,
單調遞增。
為編碼c的族的速率(rate).
是編碼C的族的相對距離。探尋
和
的關係,我們可以得到塊碼的上下界。
漢明界
Singleton界
singleton界要求塊碼的相對距離和速率之和不能大於1,換句話說就是塊碼滿足不等式:
。Reed–Solomon碼就是一個滿足singleton不等式的例子。
Plotkin界
Elias–Bassalygo界
塊碼設計
1、對於給定的n和k的值,我們希望
的值儘可能達到最大。
2、編碼的設計應當做到編解碼過程相對簡單,需要使用的記憶體和處理時間儘可能小。
3、我們希望附加比特數(n-k)比較少,以減少頻寬。
4、我們希望附加比特數(n-k)比較多,以減少差錯率。
顯然最後兩個目標是互相衝突的,所以我們在設計的時候需要折中地考慮。
編碼機制的效率
在右圖中,右邊的曲線是無編碼的調製系統,曲線左邊部分代表能夠改進的部分。在這個區域中對於給定的
(每比特信號能量與每赫茲噪聲功率密度的比值)也更小。另一條曲線是典型的編碼率為1/2(數據比特和檢驗比特數量相等)的系統。當差錯率為
時,編碼的套用使
減少了2.77dB。這個減少量稱為編碼增益(coding gain),它的定義是:如果使用相同的調製方法,要達到指定的BER,有糾錯碼的系統與無糾錯碼的系統相比較,所要求的
值的減小量(dB為單位)。
第二條編碼率為1/2的曲線BER指的是未糾正的差錯,
的值是每個數據比特的能量。因為編碼率為1/2,所以在信道上每兩個比特代表一個數據比特,即每個編碼後的比特的能量是每個數據比特能量的一般。
 編碼如何提高系統性能
編碼如何提高系統性能我們也可以看到當
小於某個閥值後,這個編碼機制反而降低了系統的性能。因為當
很小後,附加的檢查比特會給系統造成額外的負擔,它使得每個數據比特的能量減少過多,且引起差錯的增加。
 塊碼的結構
塊碼的結構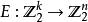

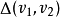
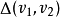


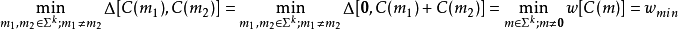





 檢測錯誤位數說明
檢測錯誤位數說明

 例子
例子
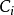
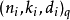
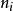








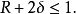


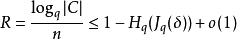

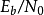

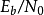
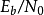

 編碼如何提高系統性能
編碼如何提高系統性能