基本介紹
故事簡介
登場人物
朝倉太陽
 朝倉太陽
朝倉太陽桐原苑生
 桐原苑生
桐原苑生諏訪巽己
 諏訪巽己
諏訪巽己作者資料
Zigzag指標

 朝倉太陽
朝倉太陽 桐原苑生
桐原苑生 諏訪巽己
諏訪巽己
zigzag(日本漫畫《ZIG ZAG浪漫宿舍》)編輯 鎖定 《ZIG ZAG浪漫宿舍》是日本女漫畫家中路有紀的漫畫作品,全9冊、原名《ZIG☆ZAG》。 [1] ...
《ZIGZAG》是麥銳娛樂旗下男生偶像廠牌MR-X繼《U&I》後在2018年7月04日發行的第二支單曲。...
ZIGZAG浪漫宿舍編輯 鎖定 本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!漫畫介紹 頭號人氣不墜、超美形NO.1 升上青風學園的朝倉太陽...
圖集 ZigZagZombie圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:落落8B2猜你關注新手上路 成長任務 編輯入門 編輯規則 ...
1 바람 (風) zigzag note 金李那 李炳浩(zigzag note) zigzag note 3:17 2 그리고 안녕 (And goodbye) 金度勛 金度勛 崔徐甲源 金度勛 3:...
《U&I》、《ZIGZAG》 [2] 目錄 1 演藝經歷 2 主要作品 3 綜藝節目 MR-X演藝經歷 編輯 2018年1月,MR-X成員李希侃、羅正、餘明君、呂晨瑜、鄧烺怡、孫...
《疾行轉彎 ZigZag》是一款虐心小遊戲。充分考驗你的反應能力和操作能力,甚至會讓你發出手指根本不夠用的感慨。遊戲操作非常簡單,通過手指點擊方向控制著小黑球一個又...
Z形試驗(zigzag test)亦稱Z形操縱試驗,是肯普夫(Kempf)在1943年首先提出來的一種衡量船舶機動性能的試驗方法。1957年以來,野本謙作和諾賓等人發展了一種對Z形試驗...
04 Strawberry ZigZagNote ZigZagNote ZigZagNote 03:33 05 따라와(Follow Me) ZigZagNote ZigZagNote ZigZagNote 03:31 06 Date (My Boy) 노는 어...
ZigZag 發行公司 PlazaVista Entertainment 製片地區 美國 導演 David S. Goyer 編劇 Landon J. Napoleon、David S. Goyer 製片人 James A. Holt 類型 劇...
《黑色星期天-Sombre Dimanche-》是ZIGZAG自製AVG獵奇文字電腦端遊戲,本遊戲以哥特恐怖因素給各位玩家帶來了意外的感受,CG由水彩畫出,給人一種獨特的感覺。遊戲裡...
《ZIGZAG》,並參與歌詞創作 [5] ;9月21日,隨MR-X發行第三首單曲《I Don’t Wanna Fight Tonight》;10月12日,參加的優酷綜藝節目《火星情報局第四季》上線...
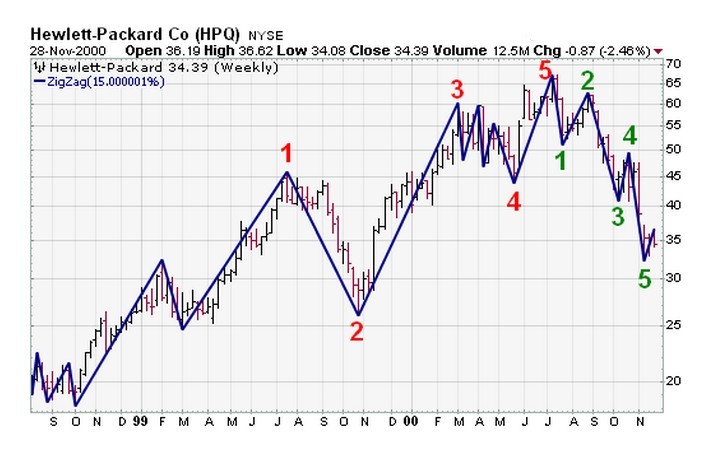
鋸齒形調整浪是波浪理論中常用的名詞,英文Zigzag,指艾略特波浪理論中最常見的一種三浪調整走勢,運行方向與更大趨勢相反,為5-3-5結構。標示為A-B-C。...
插曲《Waiting For You》 唐豆 ZigZag Note 汪小敏 插曲《等待愛》 聽海 錢雷 寧桓宇 插曲《顫抖》 林喬 金大洲 毛方圓 插曲《說你愛我》 錢麗婧 麥振鴻 吳燕珊...
