由無窮數量的多項式完全集組成的，它有兩個變數，ρ和θ，它在單位圓內部是連續正交的。需要注意的是，澤尼克多項式僅在單位圓的內部連續區域是正交的，通常在單位圓內部的離散的坐標上是不具備正交性質的。
基本介紹
- 中文名：Zernike多項式
- 變數：ρ和θ
- 作用：用來擬合光學元件表面面形
- 結構：將各項乘以相應的係數，再相加
作用,結構,用法,數學表示,函式表示,Noll序列,
作用
用來擬合光學元件表面面形
結構
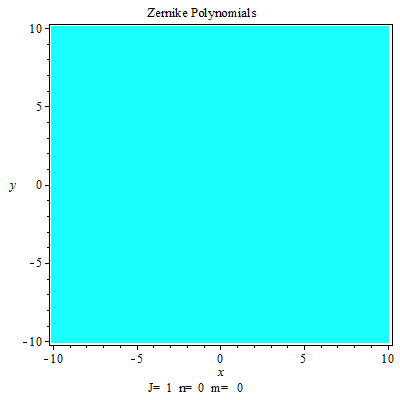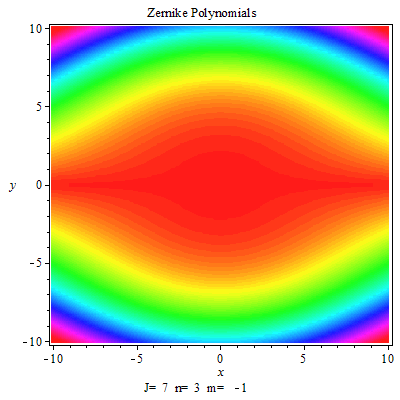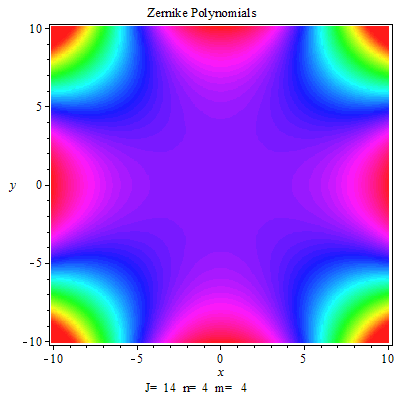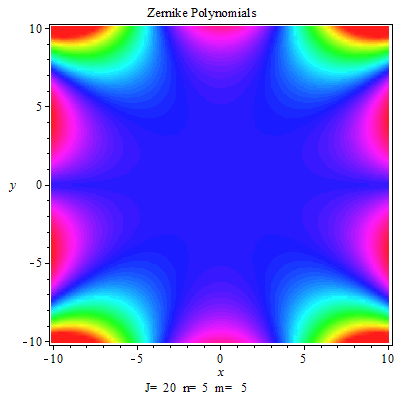
?右圖所示為多項式的各項，將各項乘以相應的係數，在相加，就得到一個三維面形數據。
不同項有不同的意義，如右面標出所示。根據不同的影響，擬合出各項係數，便可得到所求的面形。
澤尼克各項係數對應相差：
Z0 平移（piston）
Z1 x軸傾斜
Z2 y軸傾斜
Z3 離焦
Z4 X軸向像散 & 離焦
Z5 Y軸向像散 & 離焦
Z6 彗差 & x軸傾斜
Z7 彗差 & y軸傾斜
Z8 球差 & 離焦
用法
由於 Zernike多項式圓域上的正交性具有反變換和描述的圖像具有最少的信息冗餘度的特點，並且各階模式與光學設計中的Seidel像差 (如：離焦、像散、 慧差等 )係數相對應，為有選擇的處理各種像差和最佳化系統提供了有效途徑，所以在圓瞳孔徑上常作為正交基進行波前重構。
數學表示
澤爾尼克多項式分奇、偶兩類：
奇數
偶數
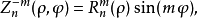
其中
為非負整數，
如果 ''n''-''m''為偶數則
:
如果''n''-''m''為奇數，則
函式表示
澤爾尼克多項式可以用超幾何函式表示
澤爾尼克多項式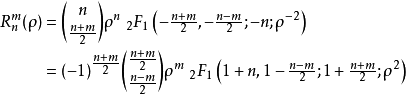
Noll序列
Noll 用一個指數 J 代表 n,m 兩個數
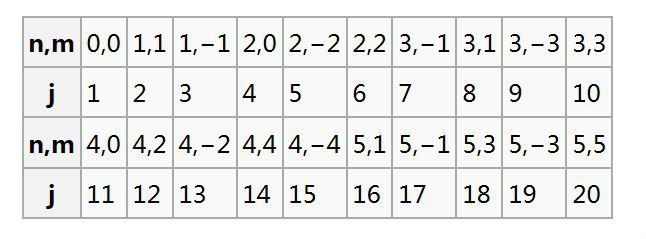澤爾尼克多項式的Noll 序列表