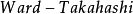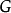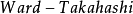若多體系統的拉氏函式具有對稱性,它在連續對稱群G的宇觀作用下不變,那么閉路格林函式將滿足一組恆等式,稱為Ward-Takahashi恆等式。
基本介紹
- 中文名:Ward-Takahashi恆等式
- 外文名:Ward-Takahashi identities
- 定義:閉路格林函式滿足一組恆等式
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:拉氏函式
概念,基本原理,
概念
令 表示場量,
表示場量, 為感興趣的複合運算元,
為感興趣的複合運算元,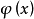 和
和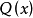 都有許多分量,組成群
都有許多分量,組成群 的表示的基。在群
的表示的基。在群 的無窮小變換下,設
的無窮小變換下,設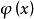 和
和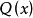 的變化規則為
的變化規則為


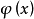
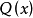


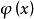
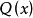


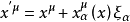
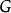
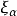
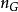
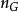

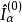
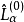


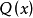
容易證明
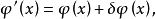
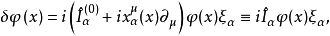


下面,我們令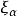 為
為 的任意無窮小函式,容易證明拉氏函式
的任意無窮小函式,容易證明拉氏函式 有下列變換關係:
有下列變換關係:
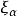


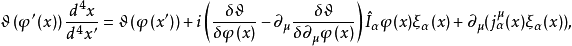
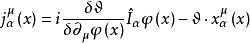
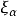


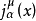
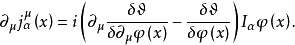
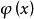

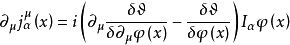
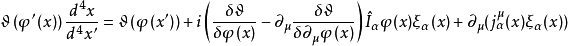
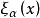
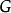
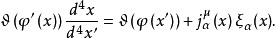

基本原理
將閉路格林函式的生成泛函寫成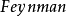 積分路徑的形式,並引進序參量
積分路徑的形式,並引進序參量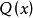 的外源
的外源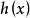 ,有
,有
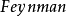
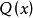
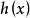
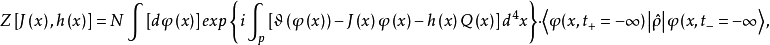


在上式中作積分變數的變換,將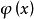 換成
換成
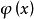


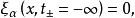

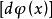
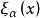
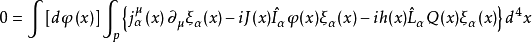
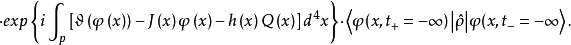
在上式第一項中作分部積分,並注意 的邊界條件,得到
的邊界條件,得到


上式就是我們求得的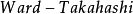 恆等式。
恆等式。