SdH震盪

在低溫和強磁場下，材料的電導率的會發生振盪的現象，Shubnikov de Haas(SdH)是物質固有的量子力學性質的巨觀表現。它經常被用來確定載流子(電子和空穴)的有效質量，使得我們能夠區分多子和少子。

基本介紹

• 中文名：SdH震盪
• 外文名：Shubnikov-de Haas oscillations

物理機制：

在足夠低的溫度和高的磁場下，金屬、半金屬或窄帶隙半導體的導電帶中的自由電子將表現為簡諧振子。當磁場強度發生變化時，簡諧振子的振盪周期呈比例變化。由此產生的能譜是由分裂的朗道能級（迴旋能所致）組成。這些朗道能級被塞曼能進一步分裂。在每個朗道能級中，迴旋能和塞曼能級以及電子狀態數(eB/h)都隨磁場的增加而線性增加。因此，隨著磁場的增大，自旋劈裂的朗道能級會向能量更高的方向移動。當每一個能級通過費米能級時，電導就會減小隨著能帶裡面的電子變為自由電子流動起來。這導致材料的輸運和熱力學相關的性能呈周期性地振盪，比如材料的電導率中，是一種可測量的振盪。由於費米“邊緣”的跨越了一系列小的能帶，所以波形是方形而不是正弦曲線，隨著溫度的降低，形狀變得越來越接近於方形。

理論：

假設一個二維電子氣體被限制在一個具有寬度和邊緣的樣品中。在磁通量密度B存在的情況下，系統的能量特徵值用朗道能級表示。如圖1所示，這些能級在垂直方向等距。每個能級在樣品內部基本上是平的(見圖1)。在樣品的邊緣，功函式向上彎曲。

圖1顯示了費米能量E_F位於兩個朗道能級之間。當能帶穿過費米能級E_F時，它們中的電子就會變得可移動。由於費米能級E_F位於兩個朗道能級之間，電子的散射只發生在向上彎曲的樣品邊緣，相對應的電子態通常被稱為邊緣通道。

圖1

該樣品中電子的輸運可以用Landauer-Buttiker公式來描述，該公式可以用來計算在1 ≤m≤n電極之間的淨電流。在它的簡化公式中，電極m的淨電流I_m用化學勢μ_m可以表示為：

（1）

其中e為電子電荷，h為普朗克常數，i為邊通道數。矩陣T_ml表示帶負電荷的粒子(如電子)從一個電極l ≠m到另一個電極m的機率。公式1中的靜電流I_m由通向電極m的電流和從m點到其它l ≠m點的電流組成。電流等於電極m處的電壓μ_m⁄e乘以每一個邊緣通道的的霍爾電導2e⁄h。

圖2展示了一個有四個電極的樣品。為了使電流在樣品中流動，我們在電極1和4之間施加一個電壓，然後在電極2和3之間測量電壓。那么假設電子首先離開電極1，然後從電極1運動到電極2，從電極2運動到電極3，從電極3運動到電極4，最後再從電極4回到電極1。從電極1到電極2的負電荷(即電子)將會形成從電極2到電極1的電流，同理，從電極2到電極3的電子將會形成從電極3到電極2的電流，其它的類似。假設沒有電子沿著更遠的路徑輸運過來，那么理想電極電子輸運的可能為：

圖2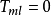

有了以上這些機率以後，通過四個電極的電流I₁...I₄，以及它們的化學勢µ₁...µ₄,之間的方程可以寫作：

電極2與電極3之間的電壓可以被測量得到，理想的電壓測試不包含從電錶裡面流過的電流，因此I₂=I₃=0，

所以，µ₂和µ₃的電勢和它們各自的電壓µ₂/e，µ₃/e使相同的，由於電極2和電極3之間沒有電壓降，電極2和電極3之間的電流I₁會發生零電阻率R_SdH。

電極2和電極3之間的電阻率為零是電子僅在樣品的邊緣通道中移動的結果。當朗道能級接近費米能量E_F時，情況就會有所不同。當電子能帶接近費米能級E_F時，這個能帶中的任何電子都會變得自由移動。因此，電子之間的散射會導致R_SdH >0。換句話說，對於費米能級附近的朗道能級，上述方法得到的電阻率為零。

套用：

SdH震盪由樣品中的二維電子密度決定。對於一個給定的磁通Ф，每個朗道能級自旋為1/2的電子的最大值為：

（2）

代入磁通量子Φ₀= h ⁄e和磁通Φ =B∙A，可得

假設N為單位面積電子狀態數的最大值，則D=N∙A

現在假設每一個朗道能級對應一個邊緣通道，對於一個給定邊緣通道的i，通道內單位面積填充電子數為N，那么單位面積電子的總數可以寫作：

單位面積電子的總數通常與樣品的電子密度相關，樣品中的電子不會無端消失，所以電子密度n為常數，則

（3）

圖3

對於給定的樣品，公式3中的電子密度n都是常數，作圖i-1/B_i，可得到一個斜率為2 ∙e/(n∙h)的直線。由於電子電荷e 和普朗克常數h是已知的,可以從圖中推導出樣品中的電子密度。在高摻雜Bi₂Se₃中可以觀察Shubnikov-de Haas振盪。圖3顯示了Bi2Se3樣品的倒數第10到第14個最小的磁通量密度倒數1/Bi。由線性擬合得到的0.00618/T的斜率為電子密度n。

Shubnikov-de Haas振盪可以用來通過確定不同套用場方向的振盪周期來繪製樣品中電子的費米表面。

相關的物理機制

這種效應與德哈斯范阿爾芬效應有關，後者是磁化過程中相應振盪的名稱。當繪製成逆磁場的函式時，每個效應的特徵都是一個周期波形。磁阻振盪的“頻率”表示在費米表面周圍的極軌道區域。費米曲面的面積用特斯拉表示。

這一效應是以約翰內斯·德·哈斯和列夫·舒勃尼科夫來命名的。