Nadolschi混沌系統

1944年，Nadolschi研究剛體運動時引入一個混沌系統其特點是方程右端含有3個非線性項，該系統稱為Nadolschi混沌系統。混沌現象是在非線性動力系統中表現的確定性、類隨機的過程，這種過程既非周期又不收斂，並且對於初始值具有敏感的依賴性。

基本介紹

• 中文名：Nadolschi混沌系統
• 外文名：nadolschi chaotic system
• 學科：控制科學與工程
• 發現者：Nadolschi
• 時間：1944年
• 類別：混沌系統

基本概念

1944年，Nadolschi研究剛體運動時引入一個混沌系統其特點是方程右端含有3個非線性項，該系統稱為Nadolschi混沌系統。混沌系統是指在一個確定性系統中，存在著貌似隨機的不規則運動，其行為表現為不確定性、不可重複、不可預測，這就是混沌現象。混沌是非線性動力系統的固有特性，是非線性系統普遍存在的現象。

表示方法

一類混沌系統(1)：

當參數取值為a=5，b=-10，c=-3.8，初值 =(-12，5，-4)時，該系統存在圖1所示的奇怪吸引子，即為混沌系統，通常被稱為Nadolschi混沌系統。

Nadolschi混沌系統同步

將式（2）作為回響系統，取式（1）為驅動系統，設計一個穩定的控制器使上述系統實現自相似結構漸近同步。式（2）為：

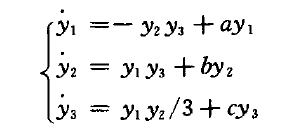
其中參數取為a=5，b=-10，C=-3.8，初值取為 =(-7，8，-11)。

在混沌同步中，用到的反饋方法主要有參數反饋和狀態變數反饋兩種。參數反饋是指利用反饋的誤差信號去調整系統的參數，使兩個混沌系統實現同步化。狀態變數反饋指的是反饋的信號直接加到回響系統的狀態變數上去，不改變系統的參數。狀態變數反饋可以有多種形式，可以是線性的，也可以是非線性的。這裡，採用線性狀態變數反饋方法設計同步控制器。

性狀態反饋控制器設計

引入狀態反饋控制的回響系統可以表示為式（3）：

由驅動系統和回響系統構成的誤差系統可以表示為式（4）：

顯然，誤差系統的原點(e1=e2=e3=0)是該系統的平衡點，因此，可以選取合適的k1，k2和k3的值，使誤差系統在零平衡點處漸近穩定，即混沌系統達到自相似結構同步。

Nadolschi混沌系統同步的充分條件

對於式（4）所示的誤差系統，當下列條件滿足時，誤差系統是漸近穩定的，即驅動系統和回響系統達到漸近同步：

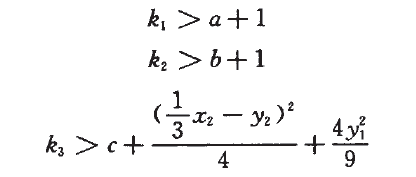
Nadolschi混沌系統的T-S模糊建模與控制

利用T-S模糊模型可以對Nadolschi混沌系統進行建模，並設計一個穩定的控制器使上述系統漸近穩定在零不動點上。

首先提出三點假設：

（1）由於混沌系統的有界性，可以定義系統狀態軌跡的研究範圍為：

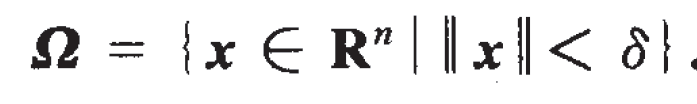
（2）混沌系統用T-S模糊模型表示時，其規則的前件變數獨立於模型的控制輸入。

（3）可以對混沌系統的每一個狀態施加反饋控制，用T-S模糊模型表示時，體現為可以用PDC方法進行有效控制。

在以上3條假設成立的前提下，當參數已知時，可以利用T-S模型表示Nadolschi混沌系統。Nadolschi混沌系統可以用包含以下4條規則的模糊模型表示：

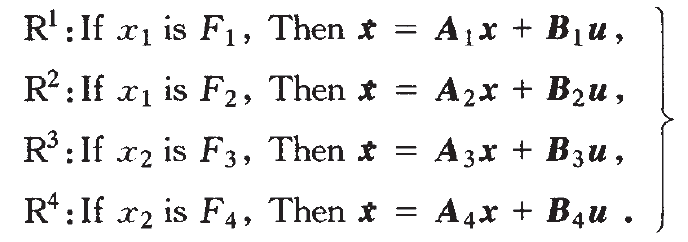
其中

模糊集合Fi(i=1，2，3，4)的隸屬度函式分別為