Look-and-say 數列

Look-and-say 數列是數學中的一種數列，它的名字就是它的推導方式：給定第一項之後，後一項是前一項的發音。

基本介紹

• 中文名：邊看邊說數列
• 外文名：Look-and-say sequence

介紹

1983年11月，在英國劍橋大學教書的著名數學家約翰·霍頓·康威(John Horton Conway) 首先發現了Look-and-say的奧秘。

規則

如果我們把 1 作為Look-and-say 數列的第一項，那么，它的前幾項是這樣的：

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...

在確定了Look-and-say 數列的第一項之後，就可以根據前一項確定後一項的值了,在上面的示例中，我們把 1 作為此種數列的第一項，那么，就可以這樣來推導它的其餘項了：

第1個是 1 時,記作 1;

第2個是讀前一個數 "2 個1", 記作 21;

第3個是讀前一個數 "1個2, 1個1", 記作 1211;

第4個是讀前一個數 "1個1,1個2,2個1", 記作 111221;

...

依此類推。

英國數學家約翰·康威(John Conway) 最早介紹和分析了Look-and-say 數列。

Look-and-say 數列和壓縮/解壓縮種的游標編碼(Run-length encoding)有相似之處。

如果我們從0到9 中的任何數字d開始，那么d將永遠是序列的最後一個數字。d不同於1，數列的開始幾項如下:

d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, …

巴黎綜合理工學院的Ilan Vardi率先研究了 d =3 的狀況， 約翰·康威(John Conway) 研究了 d=2 的情況，得出了康威常數。

基本性質

增長性

當 d =22 時，很尷尬的事情發生了，Look-and-say 數列的前幾項是：

22, 22, 22, 22,22, …

d 不等於 22 時，Look-and-say 數列可無限增長,也就是說可有無限個項。

數字出現的局限性

序列的各個項中，僅包含種子數字(上面提到的 d) 的各個數位上的阿拉伯數字 和 1，2 ，3 這三個阿拉伯數字。

宇宙衰變

康威的宇宙學定理斷言，每一個序列最終都將(“衰變”)分裂成一系列的“原子元素”，它們是有限的子序列，不再與它們的鄰居相互作用。有92個元素，其中只有1、2和3個數字，約翰·康威以鈾元素命名，稱這個序列為audioactive。還有兩個“超鈾元素”元素，分別是1、2和3。

化學元素與Look-and-say數列

增長率

在Look-and-say 數列 中，如果 表示數列的第n個成員的位數，那么存在比值極限

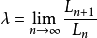
λ ≈ 1.303577269034...

這個事實由康威首先證明, 這個常數就被稱為康威常數，常用 λ 表示。除了種子數字為 22 的Look-and-say 數列，其它此類數列均存在這個極限值。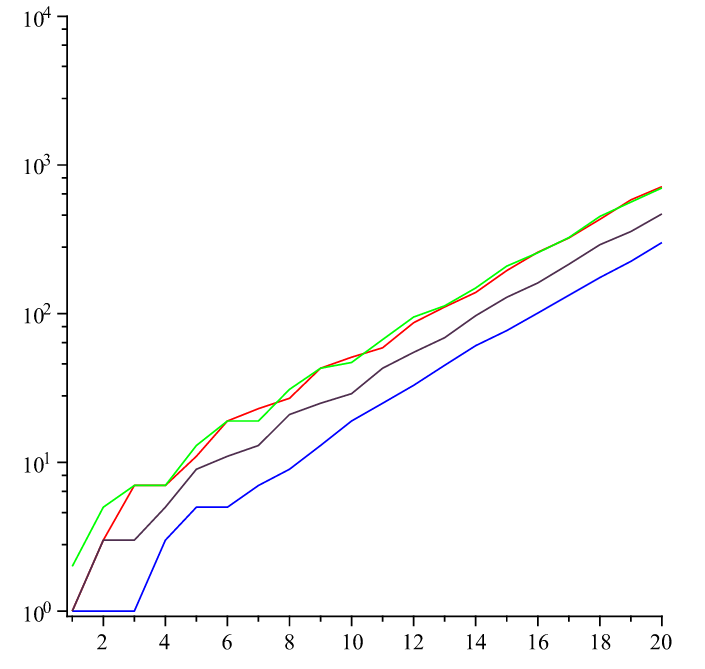

Look-and-say sequence-Conway's constant

康威常數λ 作為斜率換算為角度後，大約為 52.5075度。

康威常數還是一個 71次方多項式的唯一解。

右圖x軸為種子數(22除外)，y軸為10的n次方，

y的變化曲線的顏色代表了不同的種子數：23(紅色)、1(藍色)、13(紫色)、312(綠色)。這些曲線隨著項數的增加趨向於直線，其斜率與康威常數一致。

計算機實現

幾乎每種程式語言都可實現這個數列，這裡給出一個 Go 語言的實現。

/** @Author: suifengtec* @Date:   2017-08-22 01:55:09* @Last Modified by:   suifengtec* @Last Modified time: 2017-08-22 02:10:25**/package mainimport (    "fmt"    "math"    "strconv"    "strings")// 獲取以 1 為種子數的Look-and-say 數列任意位置的數字func getNumberOfLookAndSaySequeceSeed1(position int) int {    if position == 1 {        return 1    }    if position == 2 {        return 11    }    str := "11"    for i := 3; i <= position; i++ {        str += "$"        length := len(str)        tmp := ""        cnt := 1        for j := 1; j < length; j++ {            strSlice := strings.Split(str, "")            if strSlice[j] != strSlice[j-1] {                cntTmp := strconv.Itoa(cnt)                tmp += cntTmp                tmp += strSlice[j-1]                cnt = 1            } else {                cnt++            }        }        str = tmp    }    v, err := strconv.Atoi(str)    //v, err := strconv.ParseInt(str, 10, 64)    if err != nil {        return -1    }    if v > math.MaxInt32 {        return -1    }    return v}// 給定任意種子數 seed, 獲取 LookAndSay 數列的 第 position 項func getNumberOfLookAndSaySequece(seed int, position int) int {    if seed == 22 {        return 22    }    if position == 1 {        return seed    }    seedStr := strconv.Itoa(seed)    str := "2" + seedStr    if position == 2 {        v, err := strconv.Atoi(str)        if err != nil {            return -1        }        if v > math.MaxInt32 {            return -1        }        return v    }    for i := 3; i < position; i++ {        str += "$"        length := len(str)        tmp := ""        cnt := 1        for j := 1; j < length; j++ {            strSlice := strings.Split(str, "")            if strSlice[j] != strSlice[j-1] {                cntTmp := strconv.Itoa(cnt)                tmp += cntTmp                tmp += strSlice[j-1]                cnt = 1            } else {                cnt++            }        }        str = tmp    }    r, err := strconv.Atoi(str)    if err != nil {        return -1    }    if r > math.MaxInt32 {        return -1    }    return r}func main() {    position := 5    a := getNumberOfLookAndSaySequeceSeed1(position)    seed := 1    pos := 5    b := getNumberOfLookAndSaySequece(seed, pos)        // 111221    fmt.Println(a)    fmt.Println(b)}