基本介紹
- 中文名:局域操作和經典通訊
- 外文名:Local Operations and Classical Communications
- 縮寫:LOCC
簡介,糾纏轉換,催化轉換,塔庫定理,
簡介
例如:假設某次實驗室製備了一個貝爾態,但是卻不能確定這個貝爾態是 還是
還是 ,其中
,其中 和
和 是:
是:






A和B兩個量子位元是分隔兩地的,並且由愛麗絲對量子位元A進行操作,由鮑勃對量子位元B進行操作。首先愛麗絲測量量子位元A並得到結果0,此時我們仍不知道當初實驗室製備的貝爾態是 還是
還是 。愛麗絲藉由打電話把結果告訴鮑勃,接著鮑勃對量子位元B進行測量並得到結果0,鮑勃得知波函式塌縮成
。愛麗絲藉由打電話把結果告訴鮑勃,接著鮑勃對量子位元B進行測量並得到結果0,鮑勃得知波函式塌縮成 ,所以推得實驗室製備的貝爾態是
,所以推得實驗室製備的貝爾態是 。
。




糾纏轉換
將一個量子系統分成兩部分,利用LOCC操作,把一個糾纏態轉換成另一個糾纏態。 舉例說明:愛麗絲和鮑勃分別擁有一個糾纏態(純態)的一部分,例如 。愛麗絲和鮑勃都只能對各自的自旋進行操作,也就是Local Operation的意思。當然這個操作也包含測量,當愛麗絲進行Sz的測量後,得到本徵值+ħ/2,波函式塌縮成
。愛麗絲和鮑勃都只能對各自的自旋進行操作,也就是Local Operation的意思。當然這個操作也包含測量,當愛麗絲進行Sz的測量後,得到本徵值+ħ/2,波函式塌縮成 ,然後愛麗絲透過電話告訴鮑勃結果,這就是Classical Communications,鮑勃知道結果後也相應做了一個Local Operation,鮑勃做σx操作,於是波函式變為
,然後愛麗絲透過電話告訴鮑勃結果,這就是Classical Communications,鮑勃知道結果後也相應做了一個Local Operation,鮑勃做σx操作,於是波函式變為 。如果剛才愛麗絲測得本徵值-ħ/2,波函式塌縮成
。如果剛才愛麗絲測得本徵值-ħ/2,波函式塌縮成 ,則愛麗絲立即進行σx操作,然後經由電話告訴鮑勃,要求鮑勃不做任何操作,結果仍然可將波函式透過利用LOCC轉換成
,則愛麗絲立即進行σx操作,然後經由電話告訴鮑勃,要求鮑勃不做任何操作,結果仍然可將波函式透過利用LOCC轉換成 。
。





顯然利用 LOCC 把某個態 轉換成
轉換成 ,A與B之間的糾纏只能變小或維持不變。但是並不是只要
,A與B之間的糾纏只能變小或維持不變。但是並不是只要 的糾纏熵比
的糾纏熵比 的糾纏熵還小就必定能透過 LOCC 作轉換。要判斷可不可轉,首先,可以把
的糾纏熵還小就必定能透過 LOCC 作轉換。要判斷可不可轉,首先,可以把 和
和 分別做施密特分解:
分別做施密特分解:








將Schmidt值由大至小排列然後進行比較。尼爾森(Nielsen)在1999年提出定理:
若Majorization

對於所有 都成立,則
都成立,則 可利用LOCC轉換成 。
可利用LOCC轉換成 。


然而若上述條件不成立,並不表示 LOCC 轉換必定不成立。如果允許引入催化態,LOCC 轉換仍有可能的。
催化轉換
Jonathan 和 Plenio 在尼爾森定理髮表不久即給出一個催化轉換的例子:考慮



以上三個態已經過施密特分解且係數皆由大至小排列,以下進行 和
和 驗算係數的前
驗算係數的前 項之和(圖一):
項之和(圖一):



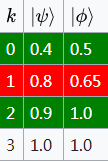 圖一
圖一以上表格中,若“ 的前
的前 項之和”比“
項之和”比“ 的前
的前 項之和”小的話,填入綠色;大的話,填入紅色;相等則是留下白色。如此一來,觀察
項之和”小的話,填入綠色;大的話,填入紅色;相等則是留下白色。如此一來,觀察 方向的顏色便一目了然。如果所有顏色皆為綠色,則表示
方向的顏色便一目了然。如果所有顏色皆為綠色,則表示 可經由LOCC轉換成
可經由LOCC轉換成 ;如果所有顏色皆為紅色,則表示
;如果所有顏色皆為紅色,則表示 可經由LOCC轉換成
可經由LOCC轉換成 ;如果顏色既有紅色又有綠色,則說明若無催化態便不可轉換。
;如果顏色既有紅色又有綠色,則說明若無催化態便不可轉換。









那么什麼是“催化轉換”和“催化態”呢?我們考慮直積態 和
和 (圖二圖三):
(圖二圖三):


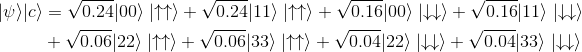 圖二
圖二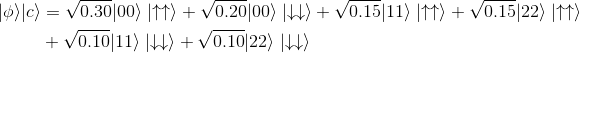 圖三
圖三以上各項已按照由大至小排列,接著同樣進行製作表格計算前 項之和(圖四):
項之和(圖四):

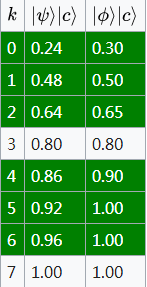 圖四
圖四塔庫定理
2007年塔庫(Turgut)證明了定理。