基本介紹
- 中文名:Kc數
- 外文名:Keulegan–Carpenter number
- 領域:物理學
簡介,湍流,流體力學,參見,
簡介
在流體力學中,Kc數(Keulegan–Carpenter number)是一個無量綱數,用來描述一個在振盪流場中的物體,所受到的粘性力相對慣性力之間的關係,也可可以用在一物體在靜止流體中振盪的情形。Kc數小表示慣性力的影響比粘性力要大,Kc數大表示(紊流)粘性力的影響較大。
Kc數的定義如下
在探討海浪對沉積物運移的影響時,會使用另一個相關的位移參數δ(displacement parameter)來表示:

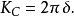
斯特勞哈爾數和Kc數有些相近。斯特勞哈爾數在形式上是Kc數的倒數。斯特勞哈爾數可以求得將一物體置入穩定的流場後,其產生旋渦分離的頻率,可以作為流場不穩定性的指標。而Kc數是和不穩定流場對物體的影響有關。
湍流
湍流(英語:turbulence),也稱為紊流(大陸地區的舊稱),是流體的一種流動狀態。當流速很小時,流體分層流動,互不混合,稱為層流,或稱為片流;逐漸增加流速,流體的流線開始出現波浪狀的擺動,擺動的頻率及振幅隨流速的增加而增加,此種流況稱為過渡流;當流速增加到很大時,流線不再清楚可辨,流場中有許多小漩渦,稱為湍流,又稱為亂流(日本及港澳台用字)、擾流或紊流。
這種變化可以用雷諾數來量化。雷諾數較小時,黏滯力對流場的影響大於慣性力,流場中流速的擾動會因黏滯力而衰減,流體流動穩定,為層流;反之,若雷諾數較大時,慣性力對流場的影響大於黏滯力,流體流動較不穩定,流速的微小變化容易發展、增強,形成紊亂、不規則的湍流流場。
流態轉變時的雷諾數值稱為臨界雷諾數。臨界雷諾數與流場的參考尺寸有密切關係。一般管道流雷諾數Re4000為湍流狀態,Re=2100~4000為過渡狀態。
有效地描述湍流的性質,至今仍然是物理學中的一個重大難題。



