Erlang噪聲又稱作伽馬(愛爾蘭)噪聲,服從了伽馬曲線的分布,是圖像處理中的一種噪聲模型。
基本介紹
- 中文名:Erlang噪聲
- 外文名:Erlang noise
- 其他名稱:伽馬噪聲、愛爾蘭噪聲、厄蘭噪聲
- 服從分布:伽瑪曲線分布
- 套用領域:圖像處理
- 實質:多個指數分布的和
概念,噪聲的分類,高斯噪聲,瑞利噪聲,伽馬噪聲,指數分布噪聲,均勻分布噪聲,脈衝噪聲(椒鹽噪聲),分布函式,噪聲實現,
概念
噪聲的分類
高斯噪聲
瑞利噪聲
瑞利噪聲是指它的機率密度函式服從瑞利分布的一類噪聲。瑞利分布(Rayleigh Distribution):當一個隨機二維向量的兩個分量呈獨立的、有著相同的方差的常態分配時,這個向量的模呈瑞利分布。
伽馬噪聲
Erlang噪聲又稱作伽馬(愛爾蘭)噪聲,服從了伽馬曲線的分布。
指數分布噪聲
均勻分布噪聲
脈衝噪聲(椒鹽噪聲)
脈衝噪聲(impulsive noise)是非連續的,由持續時間短和幅度大的不規則脈衝或噪聲尖峰組成。產生脈衝噪聲的原因多種多樣,其中包括電磁干擾以及通信系統的故障和缺陷,也可能在通信系統的電氣開關和繼電器改變狀態時產生。
分布函式
伽馬噪聲的機率密度分布函式PDF由圖給出:

.
.
其中,a>0,b為正整數且“!”表示階乘。其密度的均值和方差由下式給出:
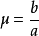
和
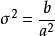
噪聲實現
伽馬噪聲的分布,服從了伽馬曲線的分布。伽馬噪聲的實現,需要使用b個服從指數分布的噪聲疊加而來。指數分布的噪聲,可以使用均勻分布來實現。
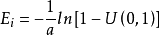
使用若干個(這裡用b表示)均勻分布疊加,就可以得到伽馬噪聲。