duffing方程

Duffing方程是描述共振現象、調和振動、次調和振動、擬周期振動、概周期振動、奇異吸引子和混沌現象(或隨機過程)的簡單數學模型。因此，在非線性振動理論中研究，Duffing方程具有重要的意義。

基本介紹

• 中文名：Duffing方程
• 外文名：Duffing

Duffing方程是非線性理論中常用的代表性微分方程，儘管是從簡單物理模型中得出來的非線性振動模型，但是其模型具有代表性。工程實際中的許多非線性振動問題的數學模型都可以轉化為該方程，特別是電工領域的一些問題的研究有重要的意義。它的標準形式為：

其中 >0為阻尼係數。g(x)是含有三次方項的非線性函式，f(x,t)為一周期函式。

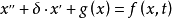
Duffing方程系統是一個典型的非線性振動系統，儘管是從簡單物理模型中得出來的非線性振動模型，但是其模型具有代表性。工程實際中的許多非線性振動問題的數學模型都可以轉化為該方程來研究，如船的橫搖運動、結構振動、化學鍵的破壞等，橫向波動方程的軸向張力擾動模型，轉子軸承的動力學方程也與Duffing系統基本相似，另外Duffing系統也非常廣泛地被套用到實際工程中，例如尖銳碰摩轉子的故障檢測、微弱周期信號檢測、電力系統周期振盪分析、周期電路系統的模擬與控制等。關於Duffing系統還有許多問題尚未徹底研究清楚，如Duffing方程的分數諧波振動、超諧波振動、組合振動等等，而且研究結果中規律性的成果可以推廣到其他類似系統。因此從某種角度來說，對非線性Duffing系統的研究是研究許多複雜動力學系統的基礎。