CS儲量積分法

CS儲量積分法（或稱儲量積分法，簡稱CS法）是以合理的圈礦模型為基礎，通過精確的數學表達和以積分為主的有關精確運算，從而實現對圈礦模型的“精確快捷定位”計算，最終求得較為可靠的礦產資源儲量的數學方法。

基本介紹

• 中文名：CS儲量積分法
• 別稱：儲量積分法
• 主要套用：礦產儲量估算方面的具體套用
• 數學依據：簡柱體新型快捷算法
• 基礎：是以合理的圈礦模型為基礎

引言

該法是CS變值方法在礦產儲量估算方面的具體套用，下面簡要介紹其有關算法。

一般來說，儲量結果的可靠程度即儲量精度(C)應同時取決於各類地質成果的可靠程度即地質精度(D)和儲量計算方法的算法精度(S)及其用法上的合理程度即用法精度(Y)，亦即C=DSY。由此可知，只有D、S、Y同時具有較高精度，才能確保獲得較高的儲量精度。其中，較高的地質精度來自較高的控制和研究程度；而較高的算法精度和用法精度則需要算法精確、用法簡便，這正是儲量計算方法的基本目標，也正是CS法的基本特點。其中，地質精度對應於礦體圈定和塊段劃分的數學模型精度。

CS法的基本思路是將儲量計算範圍內的空間實體(礦床或礦體)適當分解為有限個單元層(其形態常為層狀體)，只要求出單元層的儲量，則其總體儲量便可求和而得。因此,可最終歸結為對單元層的算法研究。一般來說，儲量計算塊段總可通過適當處理(如進行適當分解、分段或降維變換等)使之成為或比較接近各種泛柱體或正箱體（此即單元層）。這裡的降維變換是指用降低維數後的對應等值進行變換以確保變換前後的原維等值。

泛柱體是指兩底平行、側棱或側線均為連續型直線或光滑曲線的空間體。泛柱體可對應於由平行剖面或斷面(如平行斷面法)所劃分的儲量塊段。其底面可為任意形狀，各側面可為平面、曲面或扭面。這裡的扭面可由不在同一平面上的兩條導線和一條母線所決定，當導線和母線均為直線時則為線性扭面，否則，既可為非線性扭面也可為線性扭面(見正箱體)。當泛柱體的側棱或側線均為直線時叫簡柱體(如右圖1，可有五種主要類型)，否則叫雜柱體。簡柱體的底面亦可為任意形狀，但各側面只能是平面、直線型曲面或線性扭面。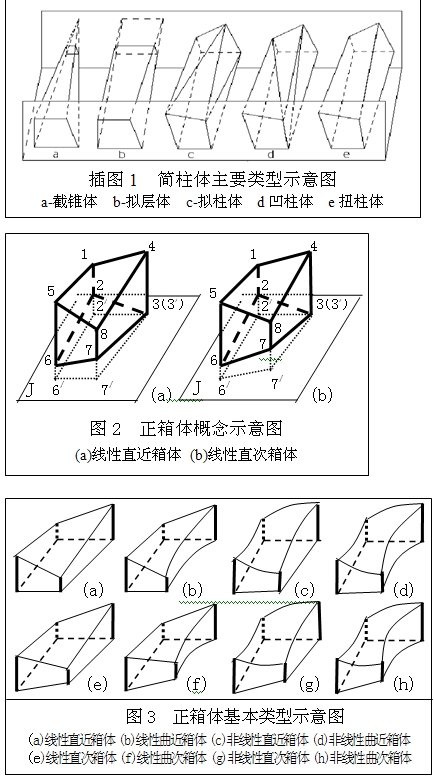

正箱體是指有四個側面同垂(或正交)於某一平面的凸棱六面體(如右圖2，J為基面)。正箱體以外的凸棱六面體叫斜箱體，二者統稱為似箱體。正箱體對應於由平行工程(如各種投影法)所劃分的儲量塊段。斜箱體可對應於由不平行工程所劃分的儲量塊段，CS法常將其適當分解後變為正箱體。正箱體可有八種基本類型(如右圖3，均為標準正箱體)，當其在基面上的投影為矩形時叫方箱體，為梯形(特殊情況為三角形)時叫近箱體，為任意四邊形時叫次箱體。當正箱體的三個共點側面為互垂平面時叫標準正箱體(常用於建立箱變坐標系)；否則，為一般正箱體(降維變換後可成標準型)。正箱體的長、寬、高分別稱為長距、寬距和高距(三者方向互垂)，其中，高距可與與單元層的正厚度和線品位相對應。這裡的正厚度和線品位對應於平行工程(正工程)中的樣品或礦體厚度和品位。正箱體中的各類近箱體也屬於泛柱體，其中的線性直近箱體則屬於簡柱體。

上述泛柱體和正箱體的數學特徵充分體現了各種單元層和礦體的局部特徵，CS法便是以此為基礎所進行的各類數學運算。其中，泛柱體常用於單元層的一元算法，正箱體常用於單元層的二元和三元算法(也可用於一元)。CS法的算法分類可歸納如下（如右圖）：

在上述分類中，線性特指正厚度和線品位均為線性變化，否則叫非線性。單元面和單元層與礦體斷面和塊段相對應，其中，單元面可由正工程控制，單元層既可由正工程控制(如正箱體)也可由正斷面控制(如泛柱體)。單元面和單元層的劃分原則應是：同一單元面和單元層的各地質變數(如正厚度、線品位等)應具有同一變化規律，以便表示為同一連續型初等函式，故其一般不宜跨層，而且常由完整單樣或單樣的某一部分所控制(即按單樣對應或厚度等比對應，此時叫基本單元面和單元層或單樣面和單樣層)，有時也可由復樣控制(叫擴元面和擴元層或復樣面或復樣層)。在上述算法分類中，基本算法為基礎和主體，主要對象為單個單元面和單元層；分解與合併算法主要用於將一個變為多個(前者)或多個變為一個(後者)，分解用於求精、合併用於簡化，其中的各種變值運算更是對該法的升華與擴展，使之套用更加廣泛、靈活，如斜箱體塊段或開採台段通常是先分解後合併。

在CS法的各類算法中，一元和二元線性類算法較為簡便和常用，合併類算法亦較常用。其中，單元面算法均較簡單，這裡從略。下面重點介紹一元和二元線性類單元層及一元合併類基本算法，余者只作簡單提示。

一元線性類單元層基本算法

本類算法的數學依據是簡柱體新型快捷算法(即簡柱體任意內插橫斷面積和體積的計算通式為一簡單的二次三項式及其定積分形式。見參考文獻)。（接右圖）

利用（1-4）、（1-5.1）、（1-5.2）和（1-6）各式便可直接求得任意內插區間[a，b]的內插塊段值，其中,體品位的求法屬於等維加權平均,相當於化學中的溶液濃度=溶質/溶液。當a=0，b=L時，可得完整單元層或完整塊段的計算結果。

此外，利用以上六種基本算式可適當設定函式值及內插區間a或b後反求內插位置或區間的b或a。

以上六種基本算式適用於正厚度和線品位均為線性變化時的簡柱體單元層，當正厚度和線品位不全為線性變化或為雜柱體時，屬一元非線性類算法，仍有上述六類基本算式。其中，正面積或面品位算式常為方次較高的整冪多項式，其它算式可仿照上述方法求之。

箱變坐標系與二元線性類單元層基本算法

單元層的二元和三元類基本算法均來自箱變坐標系。

2.1 箱變坐標系簡介

這裡先從簡單的線性扭面談起。如圖5所示(圖中的實線為一標準的線性直次箱體，也可為其它類型的標準正箱體)，該正箱體的頂面為一線性扭面，與頂面對應的高距方程為一扭面方程。當正箱體為方箱體時，其縱、橫坐標單位數各自處處對應相等，則該扭面方程不難求得；但若不為方箱體時，則其求法目前尚屬空白。這是因為其中的縱、橫坐標單位數不能各自處處對應相等，故採用常規函式無法直接對其進行精確表達。然而，若通過適當變換使原有密度均勻的非方箱體變為密度不勻的方箱體，或適當改變坐標單位使其縱、橫坐標單位數與方箱體一樣各自處處對應相等，便可按照方箱體的求法(採用坐標單位數)求出其對應的扭面方程。實現這種變換及其有關求法和算法得益於箱變坐標系、變值函式和變值運算等這一新型數學思路與方法(可叫變值方法)。現將其部分要點作一簡要說明。 箱變坐標系來自常規直角坐標系，但其同名坐標單位卻是處處可變，其坐標網是以某一標準正箱體為基準或原型(叫基箱體)，按照等比對應或變值對應進行網狀分割而成(圖5中的虛線)。分割後的平面圖形常為直邊或曲邊的梯形網(如箱面坐標系)，空間圖形常為相應的正箱網(如箱體坐標系，其中與基箱體對應的有限部分叫基準網)。當基箱體的三個基側面與三個坐標平面重合時，該箱變坐標系叫最簡坐標系或標準坐標系。此時，基箱體在三個坐標軸上的長距、寬距和高距分別稱為基長、基寬和基高，可統稱基距。CS法常採用最簡坐標系，以便簡化有關算法。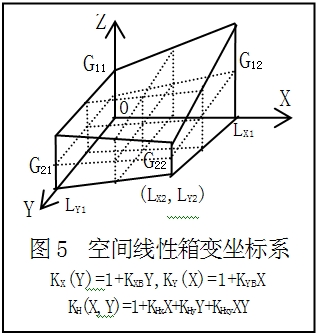

在箱變坐標系中，處處可變的坐標單位叫變值單位，其對應坐標值叫變值坐標，相應坐標系屬變值坐標系；而常規坐標系中處處相等的坐標單位叫等值單位，其對應坐標值和坐標系可叫等值坐標和等值坐標系。變值單位與某一基準單位(叫基值單位，常為同名坐標軸上的坐標單位，其對應坐標值叫基值坐標)之比叫坐標係數或變值係數，即：變值係數=變值單位/基值單位=變值坐標/基值坐標，或變值坐標=基值坐標×變值係數，此式稱為變值公式，是進行坐標變換的算法依據。變值係數可為首項為一任意非0常數的連續型初等函式(CS法常取首項為1的整式多項式)，其中，首項(KA)對應於方箱體或等值部分，餘項(R)對應於變值部分。當變值係數為1時，則變值坐標=基值坐標=等值坐標。在箱變坐標系中，同一坐標網線或網面上的同名變值坐標處處可變，而同名基值坐標或坐標單位數處處相等。為便於區別，基值坐標常用大寫字母表示(如X,Y)；求變值坐標和基值坐標的函式叫變值函式和基值函式；相應的，可把求等值坐標的函式(即常規函式)叫等值函式。前兩者的有關運算可叫變值運算。

廣義的箱變坐標系也包括斜箱坐標系在內，CS法常用最簡（或標準）正箱坐標系。其變值係數可有兩種求法：基箱法和設定法。基箱法是先求出基箱體的長距、寬距和高距算式然後除以基長、基寬和基高(即對應函式的截距)而得；設定法是根據需要直接設定變值係數，此時，只要給定一組基距便可獲得其對應的基箱體。當基箱體為直方體時可得常規的直角坐標系。最簡箱體坐標系的常用變值係數見表1（右圖）。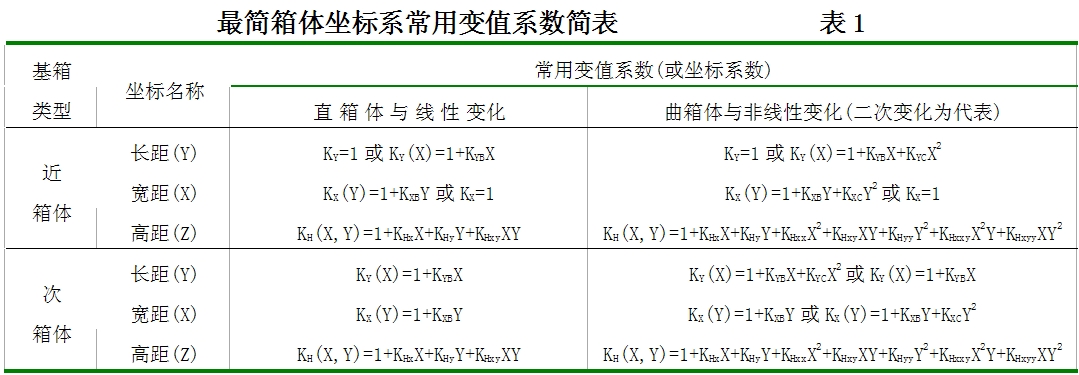

有了上述箱變坐標系，便可進行正箱體單元層的各類多元計算，下面重點說明比較常用的二元線性類算法，而對二元非線性類和三元類算法只做簡單提示。

2.2 二元線性類單元層基本算法

設某一線性單元層(如圖6,為一線性直次箱體，也可為線性直近箱體或線性曲箱體)的各類基本參數和各側面的變化特徵如表2。表中的正厚度和線品位方程可用常規數學方法求出，其中2號側面的正厚度和線品位的兩種方程完全等效，下劃線者叫同基式(與1號側面的基距相同)，無下劃線者叫異基式(與1號側面的基距不同)。試求其任意內插位置的正厚度、線品位、線品位積和任意內插區間的正面積、面品位積、面品位、體積、體品位積、體品位等基本算式。（接左面二圖片）

二元非線性類和三元類算法提示

當單元層為非線性正箱體時(如圖7，為一非線性直次箱體，也可為非線性直近箱體或非線性曲箱體)，其基本算法仍有上述九種。此時，其正厚度、線品位及坐標係數等均可為各種非線性變化，但為了便於進行有關積分運算，常可採用方次較高的整式多項式。各類基本參數和各側面的變化特徵如表3，其中，正厚度和線品位變化均以二次拋物線為例。（接右圖）

以上二元和三元類算法均屬變值運算，自變數的取值均為對應的基值坐標，故當需要自變數的實際位置(變值坐標)時，應將其對應基值坐標乘以對應變值係數。

合併類基本算法

合併類算法可有簡易近似合併與變值精確合併兩種基本算法，簡易近似合併算法是將合併後的單元面和單元層獨立進行有關運算。變值精確合併算法是利用原有基本算式進行相應的精確運算。變值合併算法(為變值函式所特有，是對常規加減運算的擴展)有同基與異基之分，同基算法與常規的加減運算規則相同，異基算法則需依據變值函式的基本性質(變值函式的自變數與基距同時擴大或縮小非0倍數，其值不變,與分數基本性質類似)進行適當變換(此時基值單位和變值係數則應擴大或縮小相應的倒數倍數)，從而使異基函式變為同基函式以便進行有關合併運算。合併類算法可有兩種：變值合併運算(變合運算)和變值合併積分運算(合積運算)。這裡以一元異基合併為例作一簡要說明(同基合併已包含其中)。（接右圖）

上式的積分與求和運算順序也可互換。當合併前的各單式為厚度類或斷面類算式時,則可利用上式進行斷面類或塊段類的同值同步精確合併。

以上兩種變值合併運算常可用於將單樣面和單樣層變為復樣面和復樣層，或將原為斜箱體的儲量塊段先分解變為正箱體然後進行合併復原的精確計算等。

上述變合與合積運算均為一元類變值合併算法，當為二元時，則應將對應的長距和寬距變數同時進行通基變換。這時還應特別注意對應變值係數的求法：先對變值係數的自變數進行通基變換，然後再乘以該自變數的通基係數。進而按照二元法求出對應還原係數。

應當注意的是，雖然變值合併後的自變數取值為同一基值坐標，但對應於合併前的實際位置卻不相同，因此，合併前的實際位置等於統一的基值坐標乘以各自通基後的變值係數。

以上變合與合積運算適用於合併後的自變數採用同值同步運算的有關情形，當自變數不需採用同值同步運算時也可不必進行通基變換。

結語

上述方法適用於一般礦產的各類儲量計算。在實際工作中，可根據實際需要和已有資料成果合理劃分單元面和單元層，靈活選擇相應算法進行各種內插計算、誤差比較等。一般來說，當正厚度和線品位為線性變化時可用線性類算法，為非線性類變化時可用非線性類算法；當單元層為泛柱體或精度要求不是很高或只需完整內插計算時可用一元類算法或簡易合併算法，當單元層為正箱體或精度要求較高或需求部分內插厚度、礦柱或礦塊時可用二元或三元類算法或變值合併算法；當只求內插結果時可用正算，需求內插位置時可用反算；進行礦山設計與開採時可採用分解與合併算法等。具體套用時，只需將工程或樣品位置及其對應正厚度、線品位或正面積、面品位等常規參數代入相應算式便可快速實現各類精確定位計算，若要計算礦石重量只需將體積乘以礦石體重即可，若要計算某一組分的重量只需將對應的體品位積乘以礦石體重或容重即可。由於該法的單元面和單元層直接對應於各種礦體斷面和塊段的地質特徵，故其用法簡便，易於保證用法精度；其被積函式直接來源於各類成果資料的精確表達和精確變換，加之各類積分運算均屬精確算法，而且,均為多項式的一次性簡單運算,從而確保了運算過程的保真度和算法精度及簡便性。其中，一元法為高精度近似算法，多元法為精確算法。經反覆驗證，當正厚度和線品位均為中等變化時，其單塊段體品位積的算法精度一般可比傳統方法提高10～30%左右或更高（如品位變化較大的頓錐體塊段）。

該法不僅適用於一般固體礦產的各類儲量計算，更可廣泛用於其它行業或領域中的各類有關問題。其中的箱變坐標系、變值函式、基值函式和變值運算等變值方法雖然只是改變一下坐標單位，所需基礎知識也並不高深，但卻從根本上揭示了某些帶有普遍性的數學規律。套用該法不僅可使廣泛存在的各種扭面及其有關的各類疑難問題迎刃而解，而且將使常規的數學空間擴展為非線性不均勻扭曲有界正負空間，也將使各種常規函式與圖象的等值運算和靜態對應擴展為各種變值函式與圖像的變值運算和動態對應等。不僅如此，上述變值方法還可再次擴展為變基等值和變基變值方法(變基是指同名基值單位處處可變，可將其視為沿坐標軸做變速運動的速度，變基時的基值坐標則為變速運動距坐標原點的路程（可對應於膨脹與收縮空間）；相應地，常規方法和前述變值方法可叫等基等值方法和等基變值方法，此時，可將基值單位視為做勻速運動的速度，等基時的基值坐標則為勻速運動距坐標原點的路程)以及其它種類的變值坐標系與相應變值函式等，從而更能揭示物質空間的相對性、複雜性和多變性以及時空之間的動態對應等客觀世界的根本規律。如此等等都將從根本上擴充了現代數學的基石，如同實數是對有理數的重大擴展一樣將是對現代數學的重大擴展，其推廣套用將有可能引起現代數學及其相關學科在思維觀念、表達方式、研究方法、套用領域等方面的某些重大突破或變革，其前景將不可估量。