比安科尼-巴拉巴西(Bianconi–Barabási)模型是網路科學中的一類無標度模型,又稱適應性模型。在巴拉巴西-阿爾伯特模型中,我們假設一個節點的成長速度完全由該節點的度決定。為了引入節點的適應性,我們假設偏好連線取決於節點的適應性η和節點度k的乘積。由此而得到的模型被稱為比安科尼-巴拉巴西模型,也被稱為適應性模型。
基本介紹
定義,生長,偏好連線,度的動態過程,度分布,等適應性,均勻分布的適應性,
定義
比安科尼-巴拉巴西模型包含以下兩個步驟:
生長
在每個時間步,網路中加入一個新節點j,該節點具有 m 條連結和適應性 。其中
。其中 是從適應性分布 ρ(η) 中採樣得到的一個隨機數。節點的適應性一旦被賦值,便不再改變。
是從適應性分布 ρ(η) 中採樣得到的一個隨機數。節點的適應性一旦被賦值,便不再改變。


網路中,每個新節點被賦予一個隨機的適應性參數,參數取值以節點顏色表示。每個新節點按照廣義偏好連線來選擇與哪些節點相連。這使得節點度的增長速度正比於其適應性。概述圖中,節點大小正比於度,隨著時間推移,適應性最高的節點將成為度最大的樞紐節點。
偏好連線
一個新節點連線到節點 i 的機率正比於節點 i 的度 ki 和適應性 ηi 的乘積:

該公式中, 和
和 的依賴關係體現了大度節點的高可見性,這意味著新節點更可能選擇和大度節點相連。
的依賴關係體現了大度節點的高可見性,這意味著新節點更可能選擇和大度節點相連。 對
對 的依賴意味著,對於度相同的兩個節點,具有更高適應性的節點會有較大的機率獲得新連結。因此,公式保證了,對於最初只有少數幾個連結的“年輕”節點而言,只要其適應性比其他節點高,也可以快速地獲得連結。
的依賴意味著,對於度相同的兩個節點,具有更高適應性的節點會有較大的機率獲得新連結。因此,公式保證了,對於最初只有少數幾個連結的“年輕”節點而言,只要其適應性比其他節點高,也可以快速地獲得連結。




度的動態過程
我們可以使用連續介質理論來預測每個節點的度隨時間的演化。根據優先連線公式,節點 i 的度的變化速度可以記為:

假設 的時間演化服從冪指數
的時間演化服從冪指數 依賴於其適應性的冪律分布:
依賴於其適應性的冪律分布:





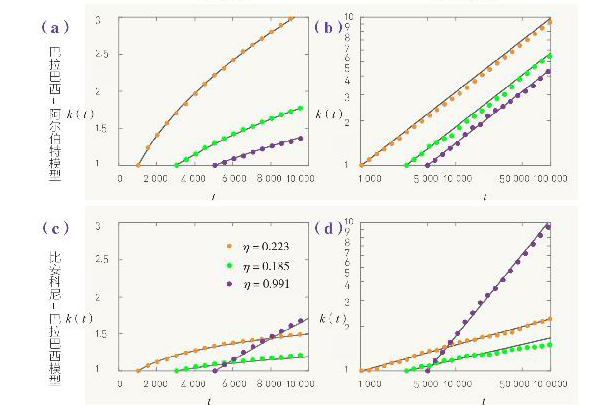
在巴拉巴西-阿爾伯特模型中, ,因此每個節點的度按照時間的平方根速度增長。而在比安科尼-巴拉巴西模型中,冪指數正比於節點的適應性
,因此每個節點的度按照時間的平方根速度增長。而在比安科尼-巴拉巴西模型中,冪指數正比於節點的適應性 ,因此每個節點具有各自的冪指數,適應性較高的節點,度增長較快。加入時間足夠長,適應性高的節點最終會將適應性低的節點甩在身後。Facebook 為該現象提夠了典型案例:具有高吸引力的一位後來者,獲得連結的速度要快於其競爭者,最終成為整個網路中最大的樞紐節點。
,因此每個節點具有各自的冪指數,適應性較高的節點,度增長較快。加入時間足夠長,適應性高的節點最終會將適應性低的節點甩在身後。Facebook 為該現象提夠了典型案例:具有高吸引力的一位後來者,獲得連結的速度要快於其競爭者,最終成為整個網路中最大的樞紐節點。


度分布
使用連續介質理論, 我們可以計算出由比安科尼-巴拉巴西模型生成的網路的度分布:





等適應性
當所有節點的適應性相同時,比安科尼-巴拉巴西模型退化為巴拉巴西-阿爾伯特模型。實際上,這個情形對應著 ,即所有節點的適應性都為
,即所有節點的適應性都為 。在這種情況下,我們根據公式可以得到
。在這種情況下,我們根據公式可以得到 ,
, 。進而,我們可以得到度分布
。進而,我們可以得到度分布 ,即巴拉巴西-阿爾伯特模型中廣為人知的度分布形式。
,即巴拉巴西-阿爾伯特模型中廣為人知的度分布形式。





均勻分布的適應性
更值得關注的是,節點適應性各不相同時該模型的表現。我們假設 均勻分布於區間
均勻分布於區間 上。在該情況下,根據公式可以得到:
上。在該情況下,根據公式可以得到:









綜上所述,比安科尼-巴拉巴西模型可以解釋這一現象:內在屬性不同的節點獲取連結的速度不同。該模型預言,節點的生長速度取決於其適應性 ,我們可以由此計算出度分布對適應性分布
,我們可以由此計算出度分布對適應性分布 的依賴關係。
的依賴關係。