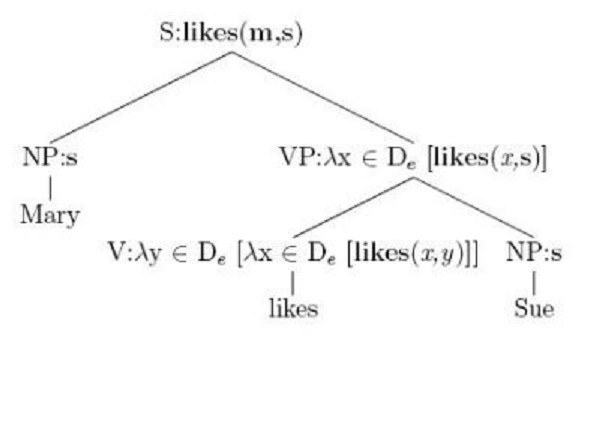
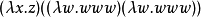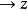在lambda演算中,一個項是beta範式(規範型),如果沒有“beta歸約”是可能的。一個項是beta-eta範式,如果既沒有beta歸約又沒有“eta 歸約”是可能的。一個項是頭部範式,如果沒有“在頭部位置的 beta-可規約式”。
基本介紹
- 中文名:Beta範式
- 外文名:Beta paradigm
- 領域:lambda演算
Beta 歸約,歸約策略,
Beta 歸約
在lambda演算中,beta可歸約式(redex)是如下形式的項
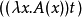
這裡的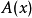 是(可能)涉及變數
是(可能)涉及變數 的項。
的項。
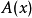

“在頭部位置的beta歸約”是把如下重寫規則套用於一個beta可歸約式
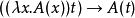
這裡的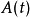 是把項
是把項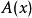 中變數
中變數 替換為項
替換為項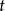 的結果。
的結果。
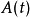
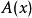

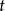
一個beta歸約在頭部位置,如果它有如下形式:
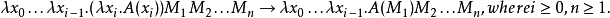
不是這種形式的任何歸約都是內部beta歸約。
歸約策略
一般的說,對於給定項有多個不同的可能的 beta 歸約。正規序歸約是一種求值策略,它始終套用“頭部位置的 beta 歸約”的規則,直到沒有更多的這種歸約是可能的。在這一點上,結果的項是“頭部範式”。
相反的,在套用序歸約中,首先套用內部歸約,而只在沒有更多的內部歸約是可能的時候套用頭部歸約。
正規序歸約是完備的,在如果一個項有頭部範式則正規序歸約總是能最終達到它的意義上。相反的,套用序歸約可能不終止,即使在這個項有規範形式的時候。例如,使用套用序歸約,下列歸約序列是可能的:
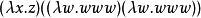
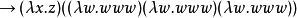
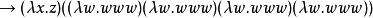
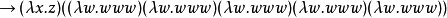
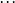
而使用正規序歸約,同樣的起點迅速的歸約到範式: