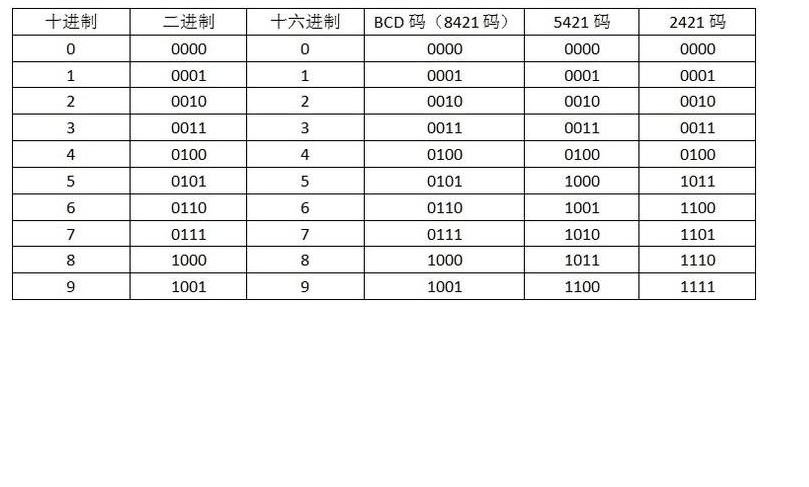
二進碼十進數(Binary-Coded Decimal,簡稱BCD,大陸稱BCD碼或二-十進制編碼)是一種二進制的數字編碼形式。
基本介紹
- 中文名:BC碼
- 外文名:Binary-Coded Decimal
- 全稱:二進碼十進數
- 作用:高精確度的計算
- 中國大陸稱法:8421碼
- 定義:一種二進制的數字編碼形式
簡述,常用編碼方式,編碼比較,共同特點,無權碼特點,區別,轉換與運算,
簡述
這種編碼形式利用了四個位元來儲存一個十進制的數碼,使二進制和十進制之間的轉換得以快捷的進行。這種編碼技巧,最常用於會計系統的設計里,因為會計制度經常需要對很長的數字串作準確的計算。相對於一般的浮點式記數法,採用BCD碼,既可保存數值的精確度,又可免卻使電腦作浮點運算時所耗費的時間。此外,對於其他需要高精確度的計算,BCD編碼亦很常用。
常用編碼方式
最常用的BCD編碼,就是使用"0"至"9"這十個數值的二進碼來表示。這種編碼方式,在中國大陸稱之為"8421碼"。除此以外,對應不同需求,各人亦開發了不同的編碼方法,以適應不同的需求。這些編碼,大致可以分成有權碼和無權碼兩種:
有權碼,如:8421(最常用)、2421、5421…
無權碼,如:餘3碼、格雷碼…
編碼比較
以下為三種常見的BCD編碼的比較。
十進數 8421-BCD碼 餘3-BCD碼 2421-A碼
(M10) D C B A C3 C2 C1 C0 a3 a2 a1 a0
0 0 0 0 0 0 0 1 1 0 0 0 0
1 0 0 0 1 0 1 0 0 0 0 0 1
2 0 0 1 0 0 1 0 1 0 0 1 0
3 0 0 1 1 0 1 1 0 0 0 1 1
4 0 1 0 0 0 1 1 1 0 1 0 0
5 0 1 0 1 1 0 0 0 0 1 0 1
6 0 1 1 0 1 0 0 1 0 1 1 0
7 0 1 1 1 1 0 1 0 0 1 1 1
8 1 0 0 0 1 0 1 1 1 1 1 0
9 1 0 0 1 1 1 0 0 1 1 1 1
共同特點
8421碼的優點是由於編碼值與字元從0到9的ASCII碼的低4位相同,有利於簡化輸出輸入過程中從字元→BCD和從BCD→字元的轉換操作,是實現人機聯繫時比較好的中間表示。需要解碼時,解碼電路也比較簡單。
8421碼的缺點是實現加減運算的規則比較複雜,在某些情況下需要對運算結果進行修正。
無權碼特點
餘三碼的優點是執行十進制數相加時可以正確的產生進位信號,而且還給減法運算帶來了方便。
餘三碼的缺點和8421碼一樣,有時也需要執行加0011的修正操作。
格雷碼的優點是從某一編碼變到下一個相鄰編碼時只有一個位的狀態發生變化,有利於得到更好的解碼波形,或者在從模擬到數字、從數字到模擬的轉換電路中得到更好的運行結果。
格雷碼的缺點是需要碼錶。
區別
壓縮BCD碼的每一位用4位二進制表示,一個位元組表示兩位十進制數。例如10010110B表示十進制數96D;非壓縮BCD碼用1個位元組表示一位十進制數,高四位總是0000,低4位的0000~1001表示0~9。例如00001000B表示十進制數8。
轉換與運算
例子1-1 將 62.142D 轉換成BCD碼。
(62.142)D = 62.142 = (01100010.000101000010)BCD
例子1-2 將10000101.001001011BCD轉換成十進制數。
(10000101.001001011)BCD = 10000111.001001011000 =(87.258)D
要將一個二進制數轉換稱BCD碼,可以先將它轉換成十進制數,然後再將十進制數轉換成BCD。同樣將BCD碼轉換稱二進制數,也是先轉換為十進制數,再轉換為二進制數。
例子1-3 將11111000100B轉換為BCD碼。
(11111000100)B = 1988D = 0001100110001000 = (0001100110001000)BCD