對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G)為ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆蓋多項式”。
基本介紹
- 中文名:點覆蓋多項式
- 所屬學科:數學
- 屬性:圖的一種多項式
- 相關概念:點覆蓋,簡單圖,覆蓋單元集等
基本介紹
相關定義












點覆蓋多項式的定義











舉例分析




























基本定理
















邊覆蓋多項式的消去定理










點覆蓋多項式的消去定理
















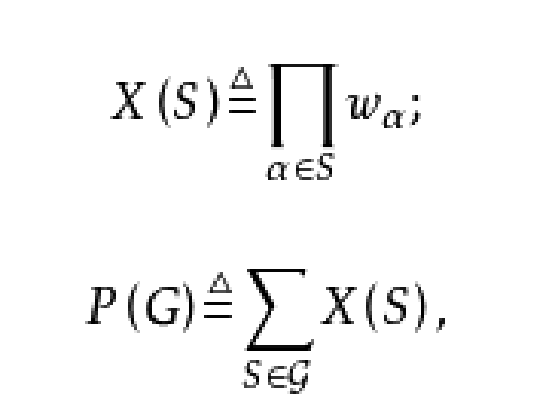
對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G)為ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆蓋多項式”。





























































































對給定的覆蓋單元集F,設圖G所有邊(點)覆蓋所構成的集族為J,對每一覆蓋S∈J,將一個單項式X(S)定義為Πα∈Swα,進而對圖G賦以一個多項式P(G)為ΣS∈JX(S),這個P(G)便稱為圖G在F之下的“邊(點)覆蓋多...
覆蓋函式有兩種,分別是全局覆蓋函式和局部覆蓋函式。當前數值流形法多採用基於全局坐標的多項式覆蓋函式(簡稱全局覆蓋函式)。部覆蓋函式使得在物理覆蓋區域內的單元剛度矩陣與單元的具體位置無關,即與單元距坐標原點的遠近無關,使剛度矩陣的...
首先,我們從算法的角度研究頂點覆蓋k-路問題,確定某些問題的算法複雜性,給出這些問題的近似算法或多項式時間的精確算法。設計k為一般情況下的頂點覆蓋k-路問題的近似算法。另一方面,我們研究頂點覆蓋k-路數。將經典圖論中的方法與機率...
圖G在 之下的點覆蓋多項式稱為“子圖多項式”,而當單元 的度量 不同時,可得一些特殊的多項式。例如雙色多項式、秩多項式、色多項式等。若令 ,其中 為連通子圖 的秩,則 就是秩多項式,其中 表示由S所成的支撐子圖的秩。
在康威重修亞歷山大多項式之後不久,人們就意識到亞歷山大的論文中關於他的多項式展示了類似的串聯關係。定義 設K是三球中的一個結。讓X是無限循環蓋的的結補的ķ。此覆蓋物可以通過切割結補體沿獲得塞弗特表面的ķ並與邊界所得歧管...
給出一組目標點或者一個目標區域,找出一組感測器使得它們的感知範圍覆蓋所有的目標點或者整個目標區域。這是關於無線感測器的一個基本問題。本項目是對最小連通感測器覆蓋等 NP 難度最佳化問題的多項式時間近似算法的設計與分析。所選出的...
許多人猜測NP厵P,即在NP中有不是多項式時間可解的問題。在直覺上如果這種問題存在的話,它就是NP中“最難的”問題。NP完全問題就是NP中最難問題的一種形式化。多項式時間歸約假定給了兩個問題類q和q0,如果存在一個確定型圖靈機...
近似算法比較經典的問題包括:最小頂點覆蓋、旅行售貨員問題、集合覆蓋等。迄今為止,所有的NP完全問題都還沒有多項式時間算法。對於這類問題,通常可採取以下幾種解題策略。(1)只對問題的特殊實例求解 (2)用動態規劃法或分支限界法求解...
