計算方法
邊界層理論計算概述
影響邊界層厚度的主要因素有:來流速度u、距板前單點O的距離x和流體的黏性(運動黏性係數)v。邊界層厚度取決於有這三個物理量所組成的無量綱數:Rex=vx/u
1、積分法:以邊界層的動量積分方程為基礎,但遇到的困難是無法求出邊界層內的速度分布,往往在計算之前先假定某種速度分布形式。
2、微分法:直接求解邊界層的偏微分方程,但在求解時須引進所謂湍流模式來定量描述雷諾應力項。
N-S方程理論計算概述
運用N-S方程理論計算黏性阻力時,應注意
1、由於RANS方法本身並不封閉,須引進所謂湍流模式來定量描述雷諾應力,能否正確給出湍流模式至關重要。
2、數值計算的方法和技巧。離散方法選取是否適當、格線劃分是否恰當以及計算格線的自動生成在數值計算至關重要。
減阻方法
當黏性流體(水、空氣、原油等) 沿一固定邊界流動時,不論是內流(如管流) 或外流(如黏性流場中運動的物體),邊界上的流速u均等於零,邊界面上的法向速度梯度du/dy則不等於零,所以存在流體對邊界的剪力τo.這邊壁剪力做功的結果就要消耗掉流體中的一部分機械能,並最終以熱量形式向周圍發散,逸散於流體。 因此,降低黏性阻力就是減少機械能的消耗,也就意味著節能。
長期以來,從航空到水下運動的廣闊領域,人們一直在尋找減少流體阻力的有效方法。減小黏性阻力,大體有以下四種作法:1、用任何一種減小壁面剪下應力的方法來減小摩阻;2、作成浸水面積小、摩阻形狀影響係數小的形狀;3、 表面作得光滑以減小粗糙度的影響;4、防止邊界層分離以減小壓力阻力。
為了實現這些作法, 舉出下列一些方法
(1)利用物體形狀保持層流流動
(2)移動表面
(3)吸入流體保持層流流動
(4)均勻噴出流體
(5)利用空氣膜
(6)彈性表面
(7)利用聚合物等添加劑
(8)利用物體形狀減小浸水面積
(9)利用物體形狀減小摩阻形狀影響係數
(10)利用光滑表面減小粗糙度的影響
(11)利用物體形狀防止端流分離
(12)利用吸入或噴出流體防止分離
(13)利用渦旋發生器或粗糙度防止分離
(14)利用變流板防止分離
(15)利用整流板控制分離
(16)磁流體力學控制邊界層
(17)表面加熱
(18)表面塗膜
其中研究較為深入的方法有以下幾種:
(1)探索物體的流線型,包括由於形體改變對保持層流邊界層的影響。希望通過型線的選擇,能“自動”保持邊界層層流流態,如果做不到這一點,則通過吸氣、增壓或其它方法“強制”保持它。
(2)隨著流體力學和高分子化學研究的進一步發展,眾多學者提出高分子稀溶液能實現黏性減阻。即當把高分子稀溶液注入物體壁面附近時(注入到流核區無效),就內流而言,最高時可使阻力係數減少40%~50%,這在各領域已有了一定的套用。但這種減阻的方法在套用時有一定的局限性,有的情況甚至是不可能的,如船舶的黏性減阻就無法通過在水中加高分子稀溶液達到目的。
(3)根據仿生學的啟示,人們發現彈性材料護面可實現黏性減阻。有實驗表明:游泳運動員游泳時穿緊身的彈性尼龍衣,比不穿游泳衣時所受的阻力要小。減阻的主要原因是此彈性邊界為柔順邊界,最理想的情況下,邊界的波動能自動與附面層的波動合拍,即所謂的同步波動,在這種情況下,流動阻力大大降低,可實現最大減阻。當然,同步程度的不同,傳遞的能量在邊界區域直接散失的能量也不同。
工程實際
簡介
當船體運動時,由於水的粘性,在船體周圍形成“邊界層”,從而使船體運動過程中受到粘性切應力作用,亦即船體表面產生了摩擦力,它在運動方向的合力便是船體摩擦阻力。另外由於水具有粘性,旋渦處的水壓力下降,從而改變了沿船體表面的壓力分布情況,這種由粘性引起船體前後壓力不平衡而產生粘壓阻力。因此,粘性阻力由摩擦阻力和粘壓阻力兩部分組成,它與船體的形狀和雷諾數密切相關。
由於船體形狀比較複雜,用理論精確計算船體的摩擦阻力尚不能付諸工程實用,為此船舶工程中仍不得不沿用傅汝德提出的相當平板假定,即船體的摩擦阻力與同速度、同長度、同濕面積的平板摩擦阻力相等。這一假定是計算船體摩擦阻力的基礎。
平板邊界層
假設順著流動方向放置一薄平板,水流以均勻速度υ流經平板,如圖所示。當水流過平板時,由於水具有粘性,故平板表面處的水質點均被吸附在平板上,平板表面上流速為零。隨著與平板表面距離y 的增加,流速逐漸增加,當y 增至某一距離δ 時,其處流速達到來流的速度值。我們稱存在粘性作用的這一薄層水流為邊界層,δ 是縱向位置x的函式,稱為界層厚度。在相應平板各處距離為δ 的點,可連成一界面,此界面稱為界層邊界。
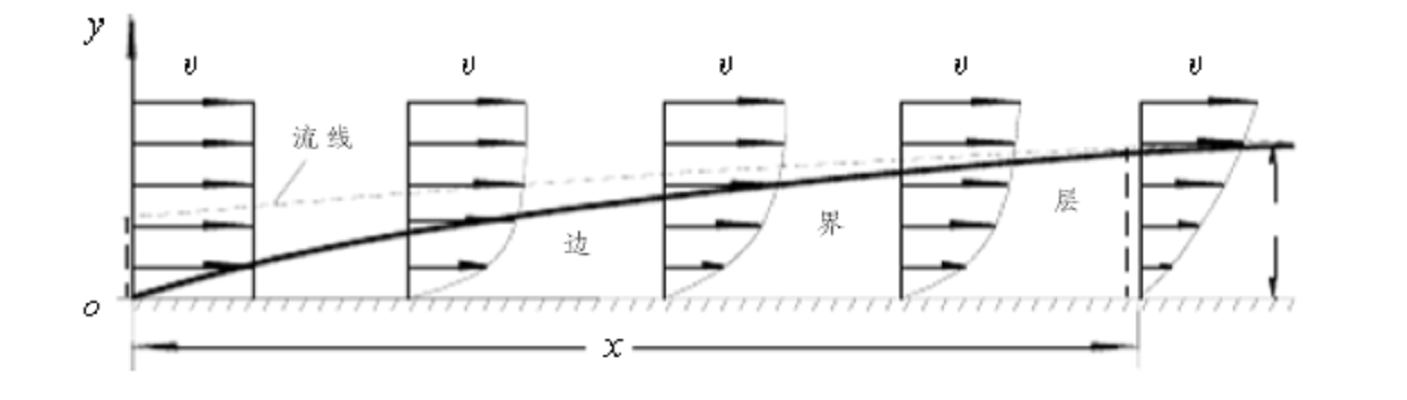 平板邊界
平板邊界應當指出,一般定義邊界層厚度常以界層內流速達到99%來流速度作為界層的邊緣,該處與板面的距離作為界層厚度值。根據實驗測定,影響邊界層厚度的主要因素是流速υ、距板前端點o的距離x和流體的粘性,即運動粘性係數ν。進一步的實驗指出δ取決於由這三個物理量所組成的無量綱數Rex=vx/u,即局部雷諾數。如果υ,x一定,當Rex很大時,則表示流體的粘性作用很小,δ就很小。理想流體可視為運動粘性係數ν = 0的實際流體,其雷諾數Re=∞,邊界層厚度δ = 0。
對邊界層內的流動狀態進行觀察研究,發現邊界層記憶體在兩種流動狀態:在平板前端部分,水質點表現有穩定的分層流動,邊界層沿板長方向增長較慢,這種流動狀態稱為層流。而在平板後部,水質點互相碰撞,運動方向極不規則,但其平均速度還是沿平板方向前進,界層厚度沿板長方向的增長較層流情況為快,這種流動稱為紊流(又稱湍流)。實際上在層流和紊流之間還有一段過渡狀態稱為過渡流或變流,如圖所示。
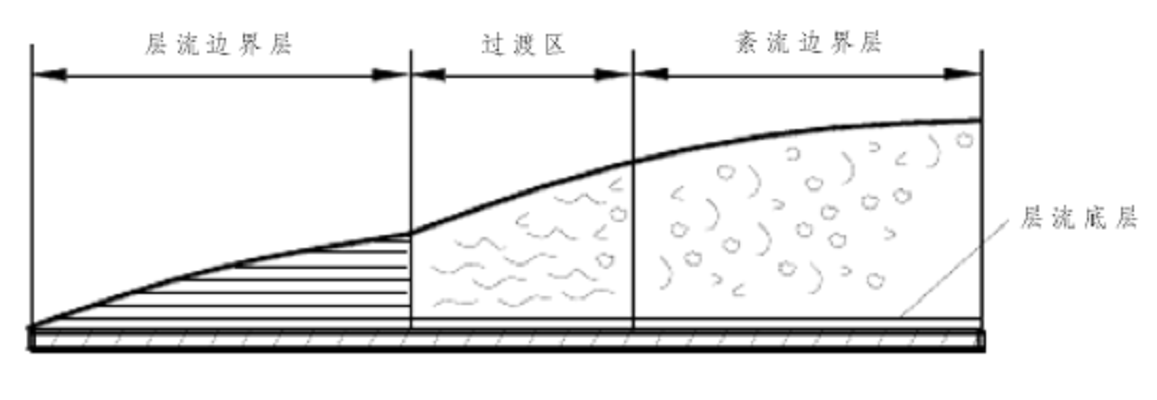 邊界層內不同流動狀態
邊界層內不同流動狀態層內的流動狀態完全取決於平板的局部雷諾數Rex:
層流狀態:Rex<(3.5~5.0)×105
過渡流: (3.5~5.0)×105 <Rex<3.0×106
湍流狀態:Rex>3.0×106
由邊界層理論求得的界層厚度為:
紊流邊界層:δ =0.0598/(lgRex-3.107)·x
邊界層理論的重要意義在於它將流體劃分為截然不同的兩部分,並加以分別處理。界層外面視為理想流體,可用勢流理論求解;界層內部則為真實流體,須用邊界層理論來研究。
需要說明的是在紊流邊界層的底部,有一極薄層水流仍為層流,稱為層流底層。這是因為在緊靠物體表面處的水質點的運動速度極低,雷諾數很小,所以呈層流狀態。
阻力成因及主要特性
由邊界層理論知,當水、空氣流經平板表面時,由於流體的粘性作用,在平板表面附近形成界層。雖然界層厚度δ極小,但界層內流體速度的變化率,即速度梯度很大。由牛頓內摩擦定律知,平板表面受到的摩擦切應力τ為:
式中 μ —— 流體的動力粘性係數;
əu/əy —— 界層內的速度梯度。
儘管所討論的介質是水,其動力粘性係數μ較小,但由於在界層內的速度梯度əu/əy很大,所以平板表面上受到的摩擦切應力不能忽略不計。由上所述,整個平板上所受到的摩擦阻力Rf 應是所有摩擦切應力的合力。
摩擦阻力與流態的關係
由上分析知,當流體介質一定時,對於給定的平板,其所受到的摩擦阻力取決於摩擦切應力τ,由上式可知τ與界層內的速度分布有關。界層內為層流和紊流時的流速分布如圖所示。在紊流邊界層中,由於水質點互相撞擊產生動量交換,以致界層內的速度分布較層流時豐滿,因此在相同來流條件下,速度梯度較大,所以其摩擦切應力必然較層流情況為大。相應的摩擦阻力係數亦大。
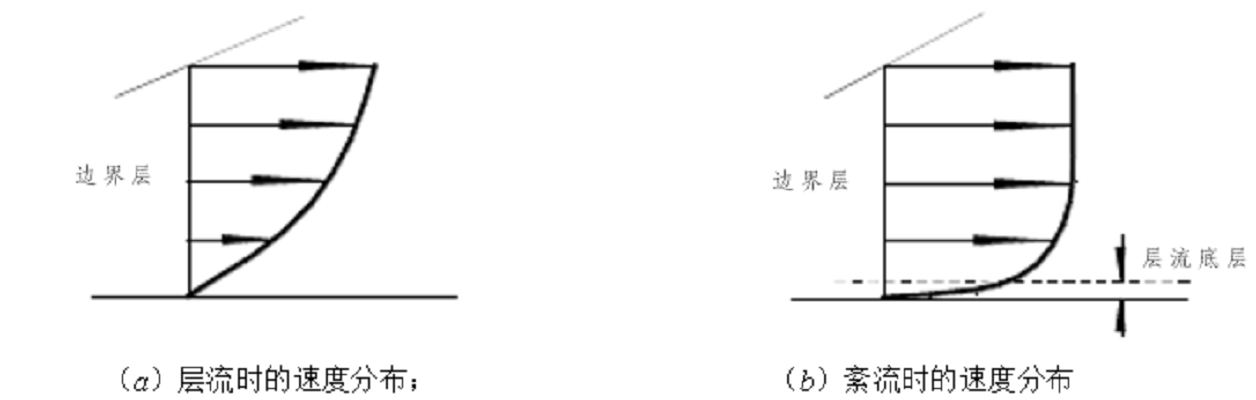 邊界層內的速度分布比較
邊界層內的速度分布比較雷諾數Re對摩擦阻力的影響
在固定流態情況下,摩擦切應力τ隨局部雷諾數Rex=vx/u變化而變化:
(1) 當來流速度υ不變時,由x增大引起Rex增大時,界層厚度增加,從而使界層內的速度分布的豐滿度有所下降,速度梯度əu/əy必然隨x增大而減小。故摩擦切應力和局部摩擦阻力係數均隨Rex增大而減小。
(2) 當x一定,由υ增大使Rex增大時,界層厚度將減薄,從而使界層內流速分布的豐滿度增大,摩擦切應力τ隨之增大。
摩擦阻力與平板濕面積的關係
如果流體介質給定,當界層內的流動狀態固定時,則意味著動力粘性係數μ和界層內的速度梯度əυ/əy均為常數,因而摩擦切應力τ亦為常數。顯然平板的摩擦阻力值正比於平板的濕面積S。這一結論對研究船體摩擦阻力具有實用意義。
船體邊界層
船體表面是個三維曲面,水流經過時,也會產生邊界層。由於船體表面縱向和橫向曲率的影響,船體周圍的三維邊界層與平板的二維邊界層有明顯的不同。其主要差別在於:
(1) 邊界層外緣勢流不同:對於平板,邊界層外緣勢流的速度和壓力均保持不變。但對於船體這兩者沿船體表而均發生變化。首先,船體表面各處的流速是不同的,船中部大於而首尾兩端卻小於船的絕對速度。根據觀察,其數值與由理想流體理論計算所得沿船體周圍的速度基本相等。如圖所示。雖然在界層以外的部分也有速度梯度和摩擦切應力,但與界層以內部分相比是很小的,所以粘性影響可以忽略不計。其次,由於外部勢流沿船體表面的流速不同,因而據伯努利方程知,沿船體表面的壓力也必不相等,船中較低,首尾較高,即存在縱向壓力梯度。
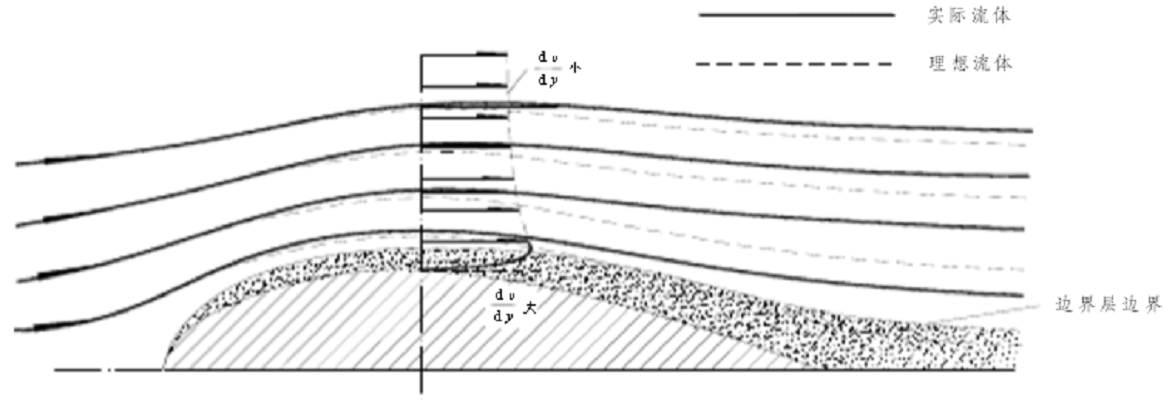 邊界層內外的速度梯度比較
邊界層內外的速度梯度比較2) 界層內縱向壓力分布不同:根據邊界層理論中界層內部壓力等於其外緣壓力的假定,甲板邊界以內縱向壓力處處相等,而船體邊界層內則存在縱向壓力梯度。即首部壓力高,中部較低而尾部又相應有所升高。由於流體的粘性作用,在這種縱向壓力分布情況下,不管尾部是否出現界層分離,均使尾部的壓力較首部壓力有所下降。因而船體不但受到摩擦阻力,而且還將受到粘壓阻力。
此外,船體邊界層在界層相對厚度以及橫向繞流對邊界層的影響等方面與平板邊界層相比亦存在差異。但是船體摩擦阻力的成因、特性與平板情況基本相同,因此船體摩擦阻力可以套用平板摩擦阻力相同的方法進行處理。
船體摩擦阻力亦可用能量觀點作解釋:就某一封閉區而言,當船在靜水中航行時,由於粘性作用,必帶動一部分水一起運動,這就是邊界層。為了攜帶這部分水一起前進,在運動過程中船體將不斷供給這部分水質點以能量,因而產生摩擦阻力。
 平板邊界
平板邊界 邊界層內不同流動狀態
邊界層內不同流動狀態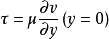
 邊界層內的速度分布比較
邊界層內的速度分布比較 邊界層內外的速度梯度比較
邊界層內外的速度梯度比較
