高斯立方體

高斯立方體是指混合高斯模型，混合高斯模型是一種參數化的機率統計方法，該模型將背景、背景內的小幅度運動以及陰影等的混合信號表示成混合高斯機率統計模型，為不同的狀態建立不同的高斯模型，採用最大似然機率來實現背景建模，並利用學習因子實時地更新背景高斯模型，適用於動態背景下的運動檢測。

基本介紹

• 中文名：高斯立方體
• 外文名：Gaussian cube
• 別名：混合高斯模型
• 定義：參數化的機率統計方法
• 適用：動態背景下運動檢測
• 套用學科：計算機原理

內容簡介

“混合高斯模型”中的“高斯”機率分布函式的曲線呈鐘形的常態分配。在一維的情況下，這是一個對稱曲線，開始時值很低，然後慢慢增長，在對稱中心達到峰值，然後再逐漸衰減。

標準K-均值聚類的模型，該模型產生一些群集，每個群集都有一個中心。一種考慮這個過程的方式是待聚類的數據符合一些基於高斯過程的機率分布，每個機率分布的均值就是群集的中心。這些機率分布給出了以高斯分布的中心作為群集質心的數據出現在空間中每一點的機率值。給定若干高斯分布，每個分布生成一個群集，這就是混合高斯模型名字的由來。

問題

把高斯分布套用到群集檢測可能會帶來兩個問題：

1、高斯分布是一維的，怎么將分布拓展到二維甚至高維?

2、高斯分布是在均值和標準差的基礎上定義的——怎么找到合適的均值和標準差?

這些問題很重要，而能夠解決這些問題正是混合高斯模型的強大之處。

多維高斯模型

高斯鐘形曲線定義了單個變數的機率分布。標準常態分配的曲線均值為0，標準差為1。簡單地再加一個變數後的機率分布就變成統計學家所稱的聯合機率分布。最終的機率圖類似於一頂帽子或者一個對稱的山峰。

對於常態分配而言，曲線下的面積是有意義的。如果想知道變數取負值的機率是多大，就需要計算一下常態分配曲線下所有負值的面積。由於曲線是對稱的，該區域的面積是總面積的50%。

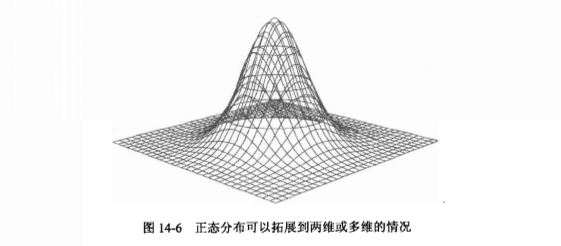
在兩維的情況下，就不再是計算曲線下的面積了，而是曲面下的體積。如果想知道兩個變數都取負值的機率有多大，就需要計算曲面下兩個值都是負數的區域的體積，結果就是總體積的25%。