體積鎖死,又稱體積閉鎖、體積自鎖等,是有限元分析過程中經常出現的一種數值問題,一般發生在完全積分單元中。由於在數值計算時不能保證體積變形為零,從而誇大體積變形剛度,導致體積鎖死。
基本介紹
- 中文名:體積鎖死
- 外文名:volumetric locking
- 別名:體積閉鎖、體積自鎖等
- 學科:數學
- 領域:數學
- 定義:有限元分析中的一種數值問題
概念,產生原因,解決辦法,
概念
體積鎖死,是有限元分析過程中經常出現的一種數值問題,一般發生在完全積分單元中。體積鎖死是指完全積分單元受到過度約束時的一種鎖死現象,如果材料是不可壓縮的或是近似不可壓縮的,完全積分單元可能會變得特別剛硬而不會產生體積變形,即所謂的“體積鎖死“。
體積鎖死的一個顯著特徵是:各個積分點之間或各個單元之間的靜水壓應力出現急劇變化。在可視化界面中繪製靜水壓應力的雲紋圖,如果看到靜水壓應力從一個積分點到另一個積分點的變化很大,呈棋盤形分布,就有可能出現了體積鎖死的數值計算問題。
產生原因
本構方程給出了固體材料的應力和應變之間的關係,通常稱為虎克定律。對於一般的各向異性材料,廣義虎克定律可以用矩陣形式表示為 ,式中,
,式中, 是材料常數張量,通常通過試驗的方法獲得。本構方程可以顯式地寫出,如圖1所示。應注意:由於
是材料常數張量,通常通過試驗的方法獲得。本構方程可以顯式地寫出,如圖1所示。應注意:由於 ,對於完全的各向異性材料總共有21個相互獨立的材料常數
,對於完全的各向異性材料總共有21個相互獨立的材料常數 ;然而對於各項同性材料,
;然而對於各項同性材料, 可以簡化成如圖1所示。
可以簡化成如圖1所示。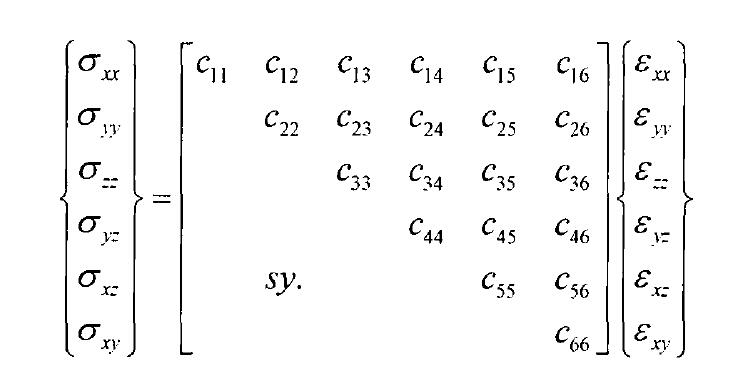





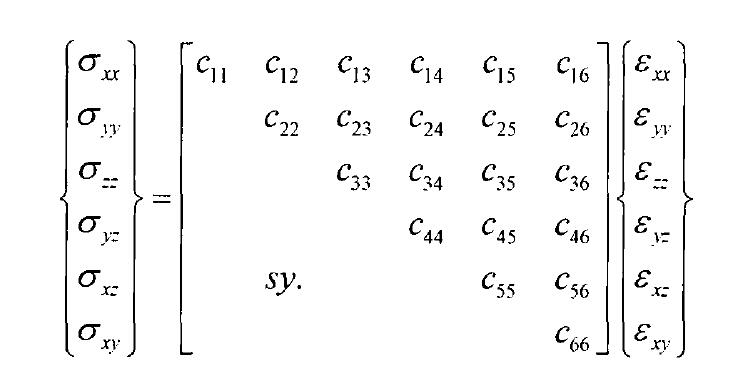
圖1 各向異性材料本構方程
式中, ;
;



上式中 分別是材料的楊氏模量,泊松比和剪下模量,這三個常數中只有兩個是獨立的。他們之間的關係是
分別是材料的楊氏模量,泊松比和剪下模量,這三個常數中只有兩個是獨立的。他們之間的關係是 。
。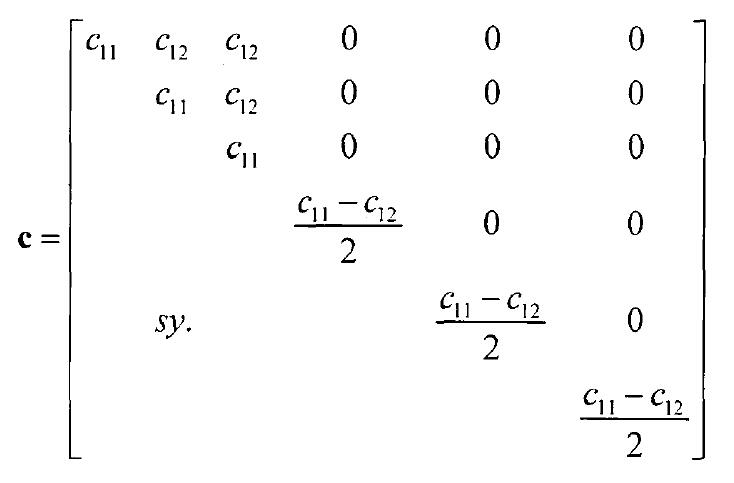


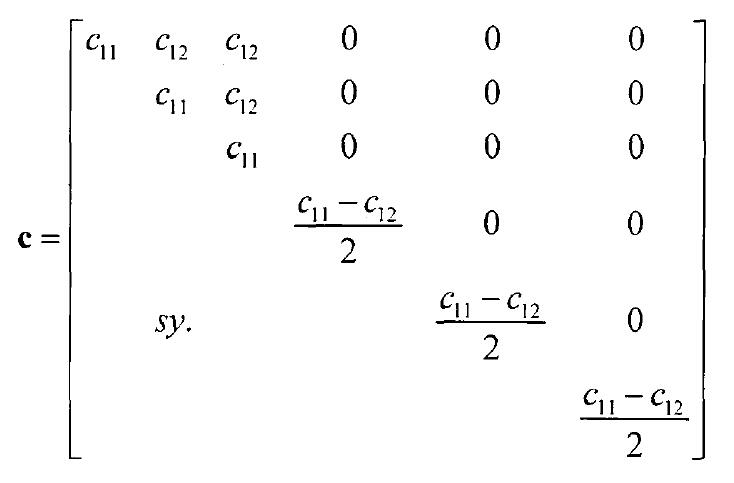
各項同性材料本構方程
由此可以注意到,當模型材料不可壓縮或幾乎不可壓縮,泊松比接近於0.5,分母上的 項趨於無窮小,從而使
項趨於無窮小,從而使 趨於無窮大,若採用全積分運算即會產生體積鎖定問題,即體積不變,體積模量太大,剛度太剛。
趨於無窮大,若採用全積分運算即會產生體積鎖定問題,即體積不變,體積模量太大,剛度太剛。


解決辦法
選取適當的單元類型
對於不可壓縮材料的有限元分析,當塑性應變與彈性應變在同一數量級上時,二次完全積分單元容易出現體積鎖死現象,往往還伴隨著沙漏模式的數值問題,因此不能用於彈塑性分析中。如果必須採用完全積分的二次實體單元,則需要選擇這種單元類型的雜交單元形式,但其計算費用大大增加。
如果使用二次減縮積分單元,當應變大於20%-40%時,需要劃分足夠密的格線才不會產生體積鎖死。
建議使用的單元類型為非協調單元、線性減縮積分單元或修正的二次四面體單元。
細化格線
在塑性應變較大的區域應劃分足夠細化的格線。
引入少量的可壓縮性
對於不可壓縮材料,適當引入少量的可壓縮性可以減輕體積鎖死的現象。幾乎不可壓縮材料和完全不可壓縮材料的計算結果很接近,因此可以將不可壓縮材料的泊松比取為0.475-0.5之間的數值。
