馬青公式由英國天文學教授約翰·馬青(John Machin ，1686 –1751)於1706年發現，他利用這個公式計算到了100位的圓周率。
馬青公式,說明,
馬青公式
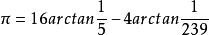
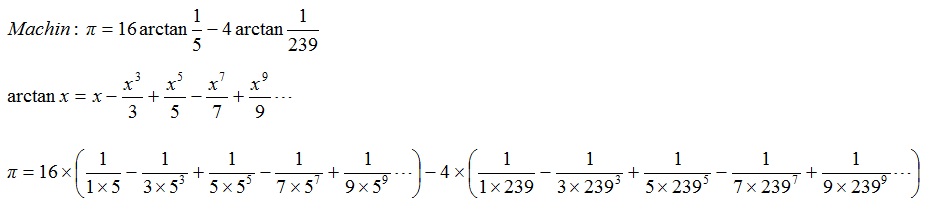
說明
馬青公式每計算一項可以得到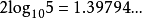
位的十進制精度。通過適當地編程，可以使它的計算過程中乘數和除數都不超過整型數據範圍，所以可以很容易地在計算機上編程實現。無需計算高精度浮點數乘法、除法或平方根，故無需使用複雜的FFT算法加速。
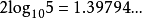
為了計算更高的十進制位數，不僅需要計算更多的項數，還要使用更長的數組來保留更高的精度。故馬青公式的時間複雜度為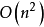
. 故此，如果要計算極多的位數，如百萬位以上，一般不使用馬青公式。
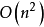
還有很多類似於馬青公式的反正切公式。在所有這些公式中，馬青公式是較為簡潔且迅速的。
用馬青公式計算Pi至小數點後100位程式
program Pi_Value;
{$APPTYPE CONSOLE}
//將Pi計算精確小數點後100位
//Machin公式
//Pi=16arctan(1/5)-4arctan(1/239)
uses
SysUtils;
const
N=100;
S=2*N+50;
aNum=5;
bNum=239;
type
Num=array [1..S] of byte;
//初始化數組
procedure AZero(var arr:Num);
var
i:smallint;
begin
for i:=1 to S do
arr:=0;
end;
//除法
procedure Division(var arr:Num;const b:smallint);
var
c,y,i:smallint;
begin
c:=0;
for i:=1 to S do
begin
y:=arr+c*10;
c:=y mod b;
arr:=y div b;
end;
end;
//加法
procedure Addition(var arr:Num;const b:Num);
var
i,y,c:smallint;
begin
c:=0;
for i:=S downto 1 do
begin
y:=arr+b+c;
if y>=10 then
begin
c:=1;
arr:=y-10;
end
else
begin
c:=0;
arr:=y;
end;
end;
end;
//減法
procedure Minus(var arr:Num;const b:Num);
var
i,y,c:smallint;
begin
c:=0;
for i:=S downto 1 do
begin
y:=arr-b-c;
if y<0 then
begin
c:=1;
arr:=10+y;
end
else
begin
c:=0;
arr:=y;
end;
end;
end;
var
tag:boolean;
a,b,Ra,Rb,t:Num;
i,j:smallint;
begin
AZero(t);
Ra:=t;Rb:=t;
tag:=true;
writeln('計算中，請等待......');
for i:=1 to N do
begin
a:=t;b:=t;
a[1]:=16;b[1]:=4;
for j:=1 to i*2-1 do
begin
Division(a,aNum);
DiVision(b,bNum);
end;
Division(a,i*2-1);
Division(b,i*2-1);
if tag then
begin
tag:=false;
Addition(Ra,a);
Addition(Rb,b);
end
else
begin
tag:=true;
Minus(Ra,a);
Minus(Rb,b);
end;
end;
Minus(Ra,Rb);
writeln('計算結果如下：');
writeln(Ra[1],'.');
for i:=2 to N+1 do
write(Ra);
readln;
End.
