馬欽凱維奇乘子定理

馬欽凱維奇乘子定理（Marcinkiewicz multiplier theorem）是給出數列為L^p(p>1)乘子的定理。

基本介紹

• 中文名：馬欽凱維奇乘子定理
• 外文名：Marcinkiewicz multiplier theorem
• 適用範圍：數理科學

簡介

馬欽凱維奇乘子定理是給出數列為L^p(p>1)乘子的定理。

它斷言：若數列{λ_k}滿足條件

則對一切p>1，{λ_k}是L^p乘子。

乘子

乘子是一種由特殊數列決定的運算元。

設P,Q分別為任意兩個周期為2π的函式類，{λ_k|k=0,±1,±2,...}是一個數列。如對於P中任一函式f的傅立葉係數{c_k|k=0,±1,±2,...}：

數列{c_kλk|k=0,±1,±2,...}總是Q中某個函式g的傅立葉係數，即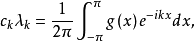

這樣，數列{λ_k}確定了一個將f∈P映到g∈Q的運算元T，使得Tf=g，此時稱T為(P,Q)乘子，也稱{λ_k}為(P,Q)乘子。

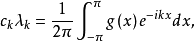
數列

數列（sequence of number）是以正整數集（或它的有限子集）為定義域的函式，是一列有序的數。

數列中的每一個數都叫做這個數列的項。排在第一位的數稱為這個數列的第1項（通常也叫做首項），排在第二位的數稱為這個數列的第2項，以此類推，排在第n位的數稱為這個數列的第n項，通常用a_n表示。