餘二面角(complementary dihedral angle)是指兩個數量相關的二面角，是指平面角互余的兩個二面角，其中任一個二面角稱為另一個二面角的餘二面角。
基本介紹
- 中文名：餘二面角
- 外文名：complementary dihedral angle
- 所屬學科：數學（立體幾何）
- 簡介：平面角互余的兩個二面角
基本概念,例題解析,二面角的平面角的求法,
基本概念
兩個二面角的平面角之和等於90°就稱這兩個二面角互余，其中任一個二面角稱為另一個二面角的餘二面角。
二面角的平面角的量數就是這個二面角的量數。二面角的平面角是幾度，這個二面角就是幾度。
也可以說兩個二面角的和等於一個直二面角時，就說這兩個二面角互為餘二面角。
例題解析
【例1】如圖，在四稜錐S-ABCD中，AD//BC且AD⊥CD；平面CSD⊥平面ABCD，CS⊥DS，CS=2AD=2；E為BS的中點，
。
圖1(1)求點A到平面BCS的距離；
(2)求二面角E-CD-A的大小。
審題要津 面對題目給出的諸多條件和諸多數據，幾乎令人“應接不暇”，因此需要梳理，需要分析，若只用綜合法，擴充信息難免有盲目性，因此還需要用分析法探索解題入口。(1)為了求點A到平面BCS的距離，若過A作平面BCS的垂線，垂足不易確定。而由A點在AD上，故可轉向證明AD//平面BCS，於是求D點到平面BCS的距離即可，(2)二面角E-CD-A的平面角也是不易作出的，注意到A-CD-S為直二面角，可知二面角E-CD-A的大小與二面角E-CD-S的大小互余，因而可以從求二面角E-CD- s的大小入手解決問題。
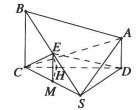圖2解: (1) ∵AD//BC，又AD不在平面BCS內，故AD//平面BCS，從而A到平面BCS的距離等於D到平面BCS的距離h。
由平面CSD⊥平面ABCD及AD⊥CD，有AD⊥平面CSD。
又BC//AD，故BC⊥平面CSD，於是DS⊥BC。
又DS⊥CS，故DS⊥平面BCS，故h=DS，以下求DS即可。
在Rt△ADS中，∵AD=1，AS=
，得
，即A到平面BCS的距離為
。
(2)在Rt△BCS中，E為斜邊中點，故BE=ES=EC=，於是BS=
。
在Rt△BCS中BC2=BS2-CS2=8-4=4，故BC=2。
在平面BCS中，引EM⊥CS於M，則有EM//BC，由E為BS中點則M為CS中點，且EM⊥平面CSD，
。
在平面CSD中，作MH⊥CD於H，則有EH⊥CD，故∠MHE為二面角E-CD-s的平面角，
且HM=CMsin∠MCH=
，由(1)知DS=，又∵CS=2，故
於是
，二面角E-CD-S為60°二面角。
∵A-CD-S為直二面角，故二面角E-CD-A的大小與60°互余，∴二面角E-CD- A大小為30°。
二面角的平面角的求法
以二面角的棱上任意一點為端點，在兩個面內分別作垂直於棱的兩條射線，這兩條射線所成的角(或叫做線性角)叫做二面角的平面角。
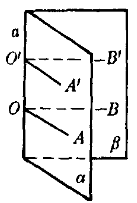圖3如圖，在二面角α-a-β的棱上任取一點O，在半平面α和β內，從點O分別作垂直於棱a的射線OA，OB，射線OA，OB組成∠AOB。在棱a上另取任意一點O′，按同樣方法作∠A′ O′B′。因為OA，OA′和OB，OB′都垂直於棱a，所以∠AOB和∠A′O′B′的兩邊分別平行且方向相同。因此∠AOB=∠A′O′B′。可見，一個二面角的所有平面角都相等，與它們的頂點在棱上的位置無關。因此，對於每一個二面角，其平面角的大小是唯一確定的。於是我們就可以藉助於二面角的平面角來度量二面角的大小。
這個定義與關於二面角大小的直觀印象相一致.若去掉定義中“與棱垂直”的條件，不管改成怎樣的兩條射線，都不會使得兩個面重合的二面角為0°，而且平二面角為180°。
如何尋找並畫出二面角的平面角，在解立體幾何題中起著重要的作用.找出二面角的平面角的方法主要有：
①根據定義求二面角的平面角。
②作二面角的棱的垂面，則垂面和二面角的兩個面的交線所成的角就是該二面角的平面角。
③根據三垂線定理或逆定理作出二面角的平面角。
④根據特殊圖形的性質作，如兩個不共面的等腰三角形若具有公共底邊，則這兩個等腰三角形底邊上的中線的夾角就是這兩個三角形所在平面組成的二面角的平面角。
