為了避免顫振事故的發生，必須通過一系列顫振風洞試驗和顫振計算對飛行器的顫振特性進行研究。顫振風洞試驗是一種高難度的特種試驗，從模型設計到專門的實驗儀器，費用高、周期長。全機跨音速顫振風洞試驗更是一項極為困難的任務。而且，顫振風洞試驗也需要藉助顫振計算對飛行器的顫振速壓進行預測、對試驗結果進行雷諾數等方面的修正研究。因此，顫振計算是當今工程上進行飛行器顫振特性研究的極其重要手段。
基本介紹
- 中文名：顫振計算
- 外文名：flutter calculation
- 學科：航空航天
- 類型：飛行術語
- 作用：飛行器顫振特性研究
- 顫振：氣動彈性力學中最重要的問題之一
顫振,研究進展,跨音速顫振計算,
顫振
顫振，彈性結構在均勻氣（或液）流中受到空氣（或液體）動力、彈性力和慣性力(見達朗伯原理)的耦合作用而發生的大幅度振動，它是氣動彈性力學中最重要的問題之一。飛行器、高層建築和橋樑等結構都可能發生顫振。顫振常導致災難性的結構破壞。1940年美國的塔科馬海峽橋因顫振而倒塌就是一個例子。顫振問題在飛行器中尤為突出。
設計飛機時，首先通過結構分析軟體在飛機的結構有限元基礎上引進空氣動力載荷，通過計算分析得到飛機的顫振速度。然後在風洞中進行模型試驗以確認顫振臨界速度。飛機樣機生產出來後，還需進行實機的飛行顫振試驗，通過實驗要求後方能定型。
為了避免顫振事故的發生，必須通過一系列顫振風洞試驗和顫振計算對飛行器的顫振特性進行研究。顫振風洞試驗是一種高難度的特種試驗，從模型設計到專門的實驗儀器，費用高、周期長。全機跨音速顫振風洞試驗更是一項極為困難的任務。而且，顫振風洞試驗也需要藉助顫振計算對飛行器的顫振速壓進行預測、對試驗結果進行雷諾數等方面的修正研究。因此，顫振計算是當今工程上進行飛行器顫振特性研究的極其重要手段。
研究進展
非定常氣動力計算的理論基礎應該說早已形成，其發展一方面取決於飛行器研製的需要，另一方面取決於計算機的能力。在早期，非定常氣動力計算主要用於動氣動彈性計算。顫振臨界點處的結構運動是簡諧振動形式，此時的非定常氣動力稱為頻域氣動力。而飛行器作任意運動時的非定常氣動力則稱為時域氣動力。時域氣動力的計算可以覆蓋頻域氣動力的計算要求，但由於時域氣動力計算複雜，率先發展起來用於工程套用的是頻域氣動力計算方法。相應地，首先發展起來的顫振計算方法則是利用頻域氣動力，在頻域裡求解結構運動方程，該方法稱為頻域法顫振計算，例如 V-g 法和 p-k 法。
上個世紀 30 年代，隨著飛機的發展，有了進行顫振計算的需求。那時的飛機，飛行速度都不高，用的都是大展弦比平直翼面。於是，首先建立起來的是基於線化理論的二維不可壓流頻域氣動力計算方法。例如，隨頻率變化的Theodorson 方法、Küssner 方法，以及不隨頻率變化的英國古典方法、前蘇聯Grossman 方法。同時，也建立了二維不可壓流時域氣動力計算方法。以後，飛機的飛行速度逐漸提高，基於線化理論的二維亞音速非定常氣動力計算方法在40 年代相繼問世。因為計算複雜，這些方法並沒有得到廣泛套用，飛機設計師們仍然用二維不可壓流的非定常氣動力來計算顫振，並用 Prandtl-Glauert 修正來處理壓縮性影響。差不多同一時期，還發展了基於線化理論的二維超音速非定常氣動力計算方法。由於超音速飛機都只能用中小展弦比翼面，難以使用二維非定常氣動力，因此這些方法並沒有得到實際套用。
上個世紀 50 年代以後，隨著跨音速飛機設計的需要和數字電子計算機的投入使用，基於線化理論的三維非定常氣動力計算方法得到發展。50 年代中期，Watkins 等人提出著名的三維亞音速頻域氣動力計算的核函式法，使三維亞音速顫振計算步入工程套用。60 年代末，Albano 等人又提出了三維亞音速頻域氣動力計算的偶極子格網法，可以處理任意外形的多翼多體組合的顫振計算。這兩種方法都得到廣泛套用。與此同時，基於線化理論的三維超音速頻域氣動力計算方法也建立起來。和亞音速範圍廣泛使用的核函式法、偶極子格網法不同，三維超音速頻域氣動力計算方法則是多種多樣，各種方法在計算精度和計算效率方面，沒有明顯的優劣，也向著多翼多體顫振計算的方向發展。基於線化理論的三維亞、超音速時域氣動力計算方法也在隨而發展，如 Green 函式法。當然，其成熟程度還遠遠趕不上頻域氣動力計算。
早在上個世紀 50 年代，跨音速飛機已經成為現實。但由於計算機能力的限制，長期以來，飛機設計師們不得不採用線化理論從亞、超音速兩邊向跨音速範圍“逼近”，再加上大量的跨音速風洞試驗驗證的方法來計算跨音速非定常氣動力。而跨音速顫振特性計算則採用凹坑餘量扣除的經驗方法進行簡化處理。直到 70 年代，隨著計算機科學和計算流體力學的發展，跨音速非定常氣動力計算方法有如雨後春筍般迅速發展，相繼建立和發展了小擾動方程、全位勢方程、Euler/N-S 方程的計算方法和軟體。小擾動方程限制較多；全位勢方程對相對簡單外形的非強激波情況更有效；Euler/N-S 方程儘管計算量大，但適用範圍廣、計算結果準確可靠，現今已經發展成為非定常氣動力計算的主流方法。基於 Euler/N-S 方程的非定常氣動力計算很費機時並且存在動態格線等問題，複雜組合體的非定常氣動力計算相比定常計算而言顯得相對不夠成熟和完善，目前仍處於不斷發展和完善之中。
跨音速時域氣動力計算迅速發展的同時，時域法顫振計算也逐漸發展起來。時域氣動力可以用於頻域法顫振計算，但更方便的是在時域內和結構運動方程耦合求解，計算出廣義坐標的時間回響以判斷飛行器是否發生顫振，該方法即為時域法顫振計算。上個世紀 90 年代初，國外開始致力於基於Euler/N-S 方程的時域法顫振計算方法研究，但由於複雜組合體跨音速顫振計算難度高、計算複雜，至今仍未完全成熟，也未見到成熟商業軟體的出現。國內也較早地開展了這方面的研究工作，但一直不能很好的處理複雜組合體問題。
跨音速顫振計算
目前工程上進行飛機顫振計算一般都採用頻域法，而其中的非定常氣動力計算均基於線性理論的偶極子格網法。跨音速區的顫振計算常採用極為粗糙的凹坑餘量扣除。但各種飛機的跨音速顫振形態很不相同，這樣的餘量扣除很難準確估計出飛機的跨音速顫振特性。發展基於非線性氣動方程的跨音速顫振計算方法是一個迫切的研究任務。
跨音速非定常氣動力計算方法分為小擾動方程、全位勢方程、歐拉方程及N-S方程解法。由它們計算得到的非定常氣動力也可用於頻域法的顫振計算。同時還可以和結構運動方程耦合求解，在時域內計算廣義坐標的回響以判斷飛機是否發生顫振。
陸志良採用二級精度的龍格-庫塔時間推進求解結構運動方程。每個時間步的時域氣動力求解採用非定常歐拉方程的雙時間有限體積推進，外時間為物理時間，與結構運動方程同步。對每個真實物理時間步採用五步Runge-Kutta時間推進進行虛擬定常疊代，此時具體解法以Jame-son的有限體積解法為基礎。
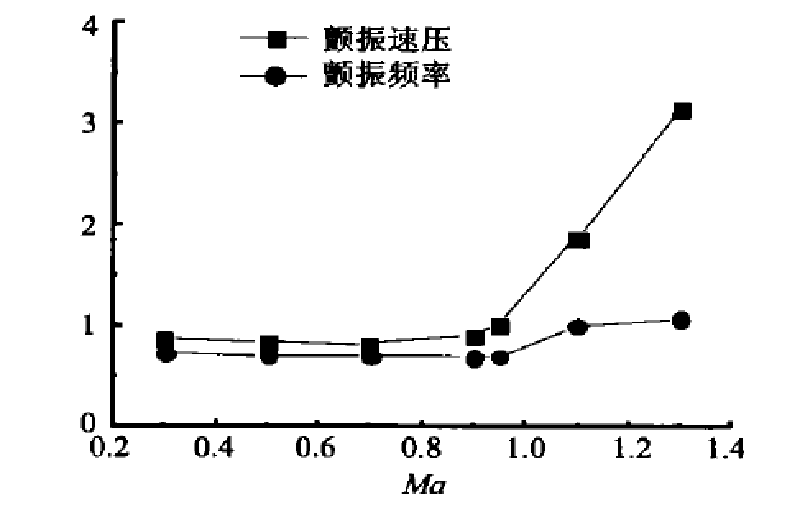
和跨音速顫振試驗類似，可壓流中，給定來流馬赫數下計算得到的顫振速壓有時存在質量不相似問題。即:此時的顫振速壓反算得到的氣流密度和飛行條件下的大氣密度可能要大很多。為給出工程實用的顫振速壓余度，必須進行密度匹配。陸志良分別採用變質量、變剛度的方法計算出質量匹配點處的顫振速壓值，並根據顫振速壓隨質量或剛度倍數的變化趨勢，得出可用的飛機跨音速顫振速壓。發展出了能用於工程實踐的飛機跨音速顫振計算方法。最後對一飛機簡化外形的跨音速顫振特性進行計算,得到了合理的計算結果。
